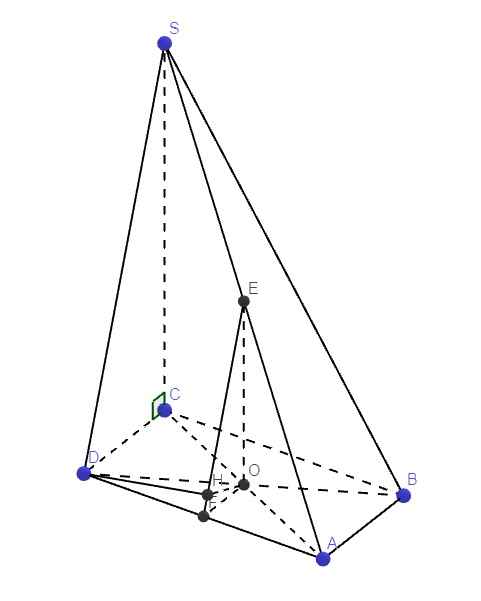
Đề đúng là SC vuông góc (ABCD) phải không nhỉ?
Gọi O là giao điểm AC và BD \(\Rightarrow\) O đồng thời là trung điểm AC và BD
Gọi E và F lần lượt là trung điểm SA và AD, từ O kẻ \(OH\perp EF\) (1)
OE là đường trung bình tam giác SAC \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}SC=\dfrac{3a}{2}\\OE||SC\Rightarrow OE\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow OE\perp AD\)
OF là đường trung bình tam giác ACD \(\Rightarrow\left\{{}\begin{matrix}OF||CD\Rightarrow OF\perp AD\\OF=\dfrac{1}{2}CD=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow AD\perp\left(OEF\right)\) \(\Rightarrow AD\perp OH\) (2)
(1);(2) \(\Rightarrow OH\perp\left(SAD\right)\)
\(\Rightarrow HD\) là hình chiếu vuông góc của OD lên (SAD)
\(\Rightarrow\widehat{HDO}\) là góc giữa BD và (SAD)
Hệ thức lượng: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}\Rightarrow OH=\dfrac{OE.OF}{\sqrt{OE^2+OF^2}}=\dfrac{3a\sqrt{10}}{20}\)
\(OD=\dfrac{1}{2}BD=\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow sin\widehat{HDO}=\dfrac{OH}{OD}=\dfrac{3\sqrt{2}}{10}\Rightarrow\widehat{HDO}\approx25^06'\)