Question

Cho hình chóp S.ABC có đáy là tam giác vuông tại A. AB = (a căn 3)/2 , AC = a/2. Tam giác SBC đều vào mặt bên ( SBC) vuông góc với mặt phẳng đáy . Biết thể tích của khối chóp S.ABC bằng (a^3)/16. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng

Answer 1

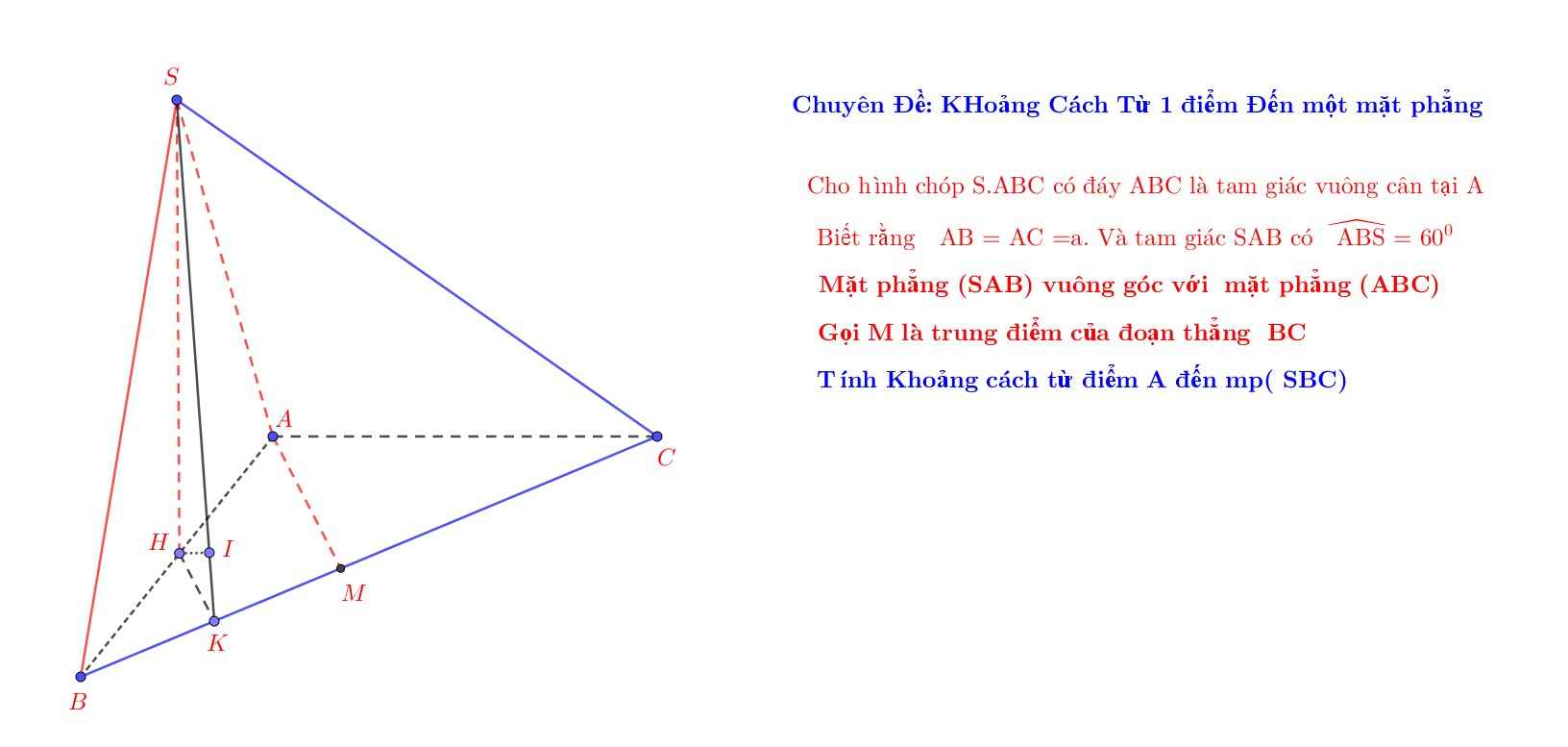
Tam giác SBC cân hay đều em nhỉ?

Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)

Answer 2

Ồ đúng rồi, mình bấm nhầm số, nhưng đề cho thừa dữ liệu thể tích chóp (hoàn toàn ko cần thiết):

Gọi H là trung điểm BC \(\Rightarrow SH\perp\left(ABC\right)\)

\(BC=\sqrt{AB^2+AC^2}=a\Rightarrow SH=\dfrac{a\sqrt{3}}{2}\) (đường cao tam giác đều cạnh a)

Gọi M là trung điểm AB \(\Rightarrow MH||AC\) (đường trung bình) \(\Rightarrow MH\perp AB\)

\(\Rightarrow AB\perp\left(SMH\right)\)

Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SAB\right)\)

\(\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)

\(MH=\dfrac{1}{2}AC=\dfrac{a}{4}\) ; \(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{MH^2}\Rightarrow HK=\dfrac{SH.HM}{\sqrt{SH^2+HM^2}}=\dfrac{a\sqrt{39}}{26}\)

Đường thẳng CH cắt (SAB) tại B, mà \(CB=2HB\)

\(\Rightarrow d\left(S;\left(SAB\right)\right)=2d\left(H;\left(SAB\right)\right)=\dfrac{a\sqrt{39}}{13}\)

Em kiểm tra lại tính toán nhé.