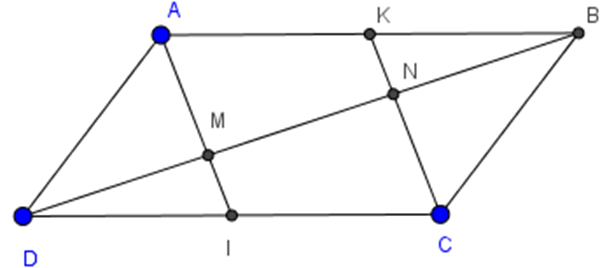
Ta có hình vẽ:
a) Ta có: AK = \(\dfrac{1}{2}\) AB
IC = \(\dfrac{1}{2}\) DC
mà AB = DC (vì ABCD là hình bình hành)
=> AK = IC
=> AK // IC (vì AB // DC)
=> AKCI là hình bình hành
=> AI // KC
b) Xét \(\Delta ABM\) có:
AK = KB (gt)
AM // KN (vì AI // KC)
=> BN = MN (1)
Xét \(\Delta DNC\) có:
DI = IC (gt)
IM // CN (vì AI // KC)
=> DM = MN (2)
từ (1) và (2) => DM = MN =NB
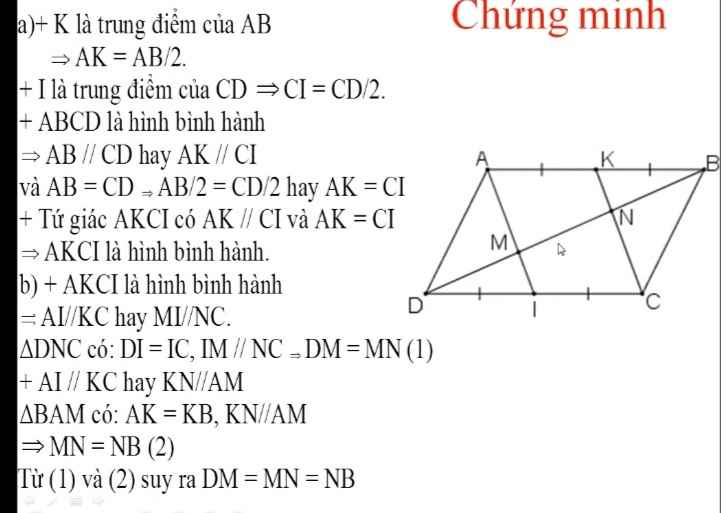
a, AK = \(\dfrac{AB}{2}\) ( K là trung điểm của AB)
CI = \(\dfrac{CD}{2}\) (I là trung điểm của CD)
AB = CD ( ABCD là hình bình hành )
suy ra : AK = CI
tứ giác AKCI có : AK // CI và AK = CI nên là hình bình hành
do đó : AI // CK
b, tam giác DNC có : IM // CN và DI = IC nên DM = MN
tam giác AMB có : KN // AM và AK = KB nên MN = NB
ta có : DM = MN và MN = NB
suy ra : DM = MN = NB
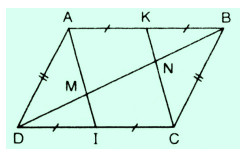
a) Tứ giác ABCD có \(AB = CD, AD = BC\) nên là hình bình hành.
Tứ giác AICK có \(AK // IC, AK = IC\) nên là hình bình hành.
Do đó \(AI // CK\)
b) \(∆DCN\) có \(DI = IC, IM // CN.\)
(vì \(AI // CK\)) nên suy ra \(DM = MN\)
Chứng minh tương tự đối với \(∆ABM\) ta có \(MN = NB\)
Vậy \(DM = MN = NB\)
a) Vì ABCD là hình bình hành (gt)
⇒{AB=CDAB//CD⇒{AB=CDAB//CD
(tính chất hình bình hành)
Mà I, K theo thứ tự là trung điểm của CD, AB (gt)
⇒{AK=AB2IC=DC2⇒{AK=AB2IC=DC2
(tính chất trung điểm)
⇒AK=IC,DI=IC⇒AK=IC,DI=IC
Lại có: AB//DC(cmt)⇒AK//ICAB//DC(cmt)⇒AK//IC
Tứ giác AICK có:
{AK//ICAK=IC(cmt){AK//ICAK=IC(cmt)
⇒⇒ Tứ giác AICK là hình bình hành (dấu hiệu nhận biết hình bình hành)
⇒AI//CK⇒AI//CK (tính chất hình bình hành)
b) ∆DCN có DI = IC (cmt), IM // CN (vì AI // KC)
⇒⇒ DM = MN (1) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)
Xét ∆ABM có AK = KB (cmt) và KN // AM ( vì AI // CK )
⇒MN=NB⇒MN=NB. (2) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)
Từ (1) và (2) ⇒DM=MN=NB.
cho tam giác ABC (AB nhỏ hơn AC),đường cao AH.gọi D,E,F lần lượt là trung điểm của các cạnh a) chứng minh rằng tứ giác BDEF là hình bình hành b) chứng minh tứ giác EFHD là hình thang cân c) Gọi I là trung điểm DF ,G là trọng tâm tam giác ABC,Cmr:4 điểm B,I,G,E thẳng hàng