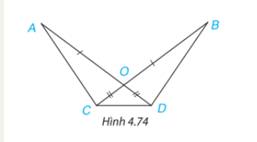
Cách 1:
a) Xét \(\Delta ACO \) và \(\Delta BDO\) có:
AO=BO (gt)
\(\widehat {AOC} = \widehat {BOD}\) (đối đỉnh)
OC=OD (gt)
=>\(\Delta ACO = \Delta BDO\)(c.g.c)
=>AC=BD (hai cạnh tương ứng)
b)Xét \(\Delta ACD\) và \(\Delta BDC\) có:
AO=BO (gt)
CO=DO (gt)
AC=BD (cmt)
=>\(\Delta ACD = \Delta BDC\)(c.c.c)
Cách 2:
a),b) Ta có: OA = OB, OD = OC nên \(OA+OD=OB+OC\) hay \(AD=BC\).
Do OC=OD nên \(\Delta OCD\) cân tại O => \(\widehat {OCD} = \widehat {ODC}\)
Xét \(\Delta ACD \) và \(\Delta BDC\) có:
AD=BC (cmt)
\(\widehat {OCD} = \widehat {ODC}\) (cmt)
CD chung
=>\(\Delta ACD = \Delta BCD\)(c.g.c)
=>AC=BD (hai cạnh tương ứng)