Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.
Luyện tập chung trang 85
Bài 4.29 (SGK Kết nối tri thức với cuộc sống trang 86)
Thảo luận (1)
Bài 4.30 (SGK Kết nối tri thức với cuộc sống trang 86)
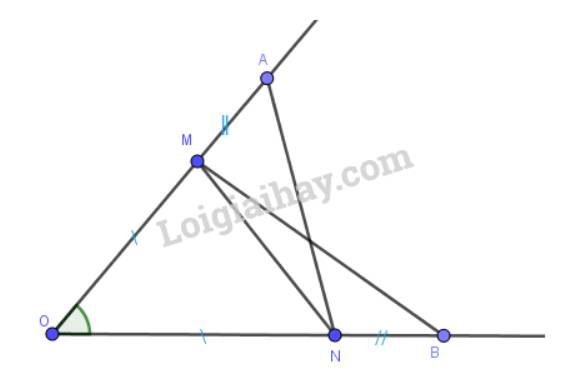
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.
Chứng minh rằng:
a) \(\Delta \)OAN = \(\Delta \)OBM;
b) \(\Delta \)AMN = \(\Delta \)BNM.
Thảo luận (1)Hướng dẫn giải
a) Xét \(\Delta OAN\) và \(\Delta OBM \) có:
OA=OB (gt)
\(\widehat{O}\) chung
OM=ON (gt)
=>\(\Delta OAN = \Delta OBM\)(c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM ( 2 cạnh tương ứng); \(\widehat {OAN} = \widehat {OBM}\)( 2 góc tương ứng) =>\(\widehat {NAM} = \widehat {MBN}\)
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét \(\Delta AMN\) và \(\Delta BNM\) có:
AN=BM (cmt)
\(\widehat {NAM} = \widehat {MBN}\) (cmt)
AM=BN (cmt)
=>\(\Delta AMN = \Delta BNM\)(c.g.c)
(Trả lời bởi Kiều Sơn Tùng)
Bài 4.31 (SGK Kết nối tri thức với cuộc sống trang 86)
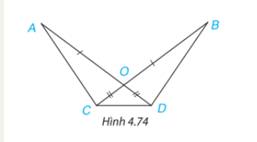
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) \(\Delta \)ACD = \(\Delta \)BDC.
Thảo luận (1)Hướng dẫn giảiCách 1:
a) Xét \(\Delta ACO \) và \(\Delta BDO\) có:
AO=BO (gt)
\(\widehat {AOC} = \widehat {BOD}\) (đối đỉnh)
OC=OD (gt)
=>\(\Delta ACO = \Delta BDO\)(c.g.c)
=>AC=BD (hai cạnh tương ứng)
b)Xét \(\Delta ACD\) và \(\Delta BDC\) có:
AO=BO (gt)
CO=DO (gt)
AC=BD (cmt)
=>\(\Delta ACD = \Delta BDC\)(c.c.c)
Cách 2:
a),b) Ta có: OA = OB, OD = OC nên \(OA+OD=OB+OC\) hay \(AD=BC\).
Do OC=OD nên \(\Delta OCD\) cân tại O => \(\widehat {OCD} = \widehat {ODC}\)
Xét \(\Delta ACD \) và \(\Delta BDC\) có:
AD=BC (cmt)
\(\widehat {OCD} = \widehat {ODC}\) (cmt)
CD chung
=>\(\Delta ACD = \Delta BCD\)(c.g.c)
=>AC=BD (hai cạnh tương ứng)
(Trả lời bởi Hà Quang Minh)
Bài 4.32 (SGK Kết nối tri thức với cuộc sống trang 86)
Cho tam giác MBC vuông tại M có \(\widehat B\) = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Thảo luận (1)Hướng dẫn giải
Xét \(\Delta CMB\) và \(\Delta CMA\) có:
MC chung
\(\widehat{BMC}=\widehat{AMC}(=90^0)\)
MB=MA (gt)
=> \(\Delta CMB = \Delta CMA\)(c.g.c)
=> CA = CB (2 cạnh tương ứng).
=> Tam giác ABC cân tại C.
Mà \(\widehat B=\) 60o
=> Tam giác ABC đều.
(Trả lời bởi Kiều Sơn Tùng)