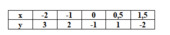
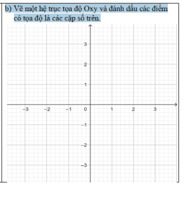
Ta có:y=f(x)=\(\dfrac{x+2}{x-1}\)
a)ĐKXĐ:x-1\(\ne0\)=>x\(\ne1\)
Vậy ĐKXĐ:\(x\ne1\)
b)Để f(x)=0 thì \(\dfrac{x+2}{x-1}\)=0=>x-2=0=>x=2(thỏa mãn ĐKXĐ)
Vậy để f(x)=0 thì x=2
c)Để f(x)>0 thì \(\dfrac{x+2}{x-1}\)>0
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2>0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+2< 0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\)=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-2\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x< -2\\x< 1\end{matrix}\right.\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\)
Vậy để f(x)>0 thì x>1 hoặc x<-2
a, Để hàm số được xác định thì \(x-1\ne0\Rightarrow x\ne1\)
Vậy......
b, Ta có:
\(f\left(x\right)=0\) \(\Rightarrow\dfrac{x+2}{x-1}=0\)
\(\Rightarrow x+2=0\Rightarrow x=-2\)
c, Để \(f\left(x\right)>0\) thì
\(\dfrac{x+2}{x-1}>0\Rightarrow x+2>0\Rightarrow x>-2\)
Vậy........
Chúc bạn học tốt!!!
a, Để hàm số xác định được giá trị khi: \(x-1\ne0\Rightarrow x\ne1\)
Vậy.........
b, \(\dfrac{x+2}{x-1}=0\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
Vậy...........
c, f(x) > 0 \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2>0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+2< 0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-2\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x< -2\\x< 1\end{matrix}\right.\end{matrix}\right.\)
Vậy f(x) > 0 <=> x > 1 và x < -2