Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
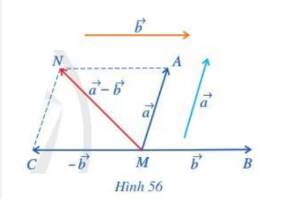
a) Đặt D, E lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Ta có: \(\overrightarrow {MA} = \overrightarrow a \)hay \(\overrightarrow {MA} = \overrightarrow {DE} \)
\( \Leftrightarrow MAED\) là hình bình hành.
Do đó A là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \)và điểm M.
Tương tự ta có:
B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \)và điểm M.
Lại có: \(\overrightarrow {MC} = - \overrightarrow b = - \overrightarrow {MB} \) do đó \(MC = MB\) và hai vecto \(\overrightarrow {MB} ,\overrightarrow {MC} \) ngược hướng nhau.
Hay M là trung điểm đoạn thẳng BC.

b) Lấy N là đỉnh thứ tư của hình bình hành AMCN.
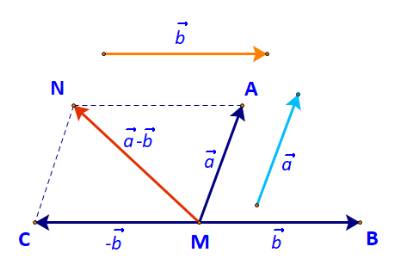
Khi đó ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \)
Mà: \(\overrightarrow {MA} = \overrightarrow a ;\;\overrightarrow {MC} = - \overrightarrow b \)
\( \Rightarrow \overrightarrow a + ( - \overrightarrow b ) = \overrightarrow {MN} \).