Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.
Cho ba điểm D, E, G. Vecto \(\overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} )\) bằng vecto nào sau đây?
A. \(\overrightarrow {EG} \)
B. \(\overrightarrow {GE} \)
C. \(\overrightarrow {GD} \)
D. \(\overrightarrow {ED} \)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} = a\), \(\overrightarrow {BC} = b\)
b) Tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto nào?
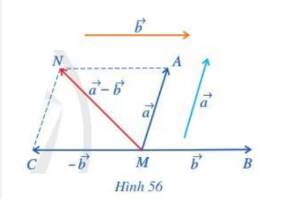
Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
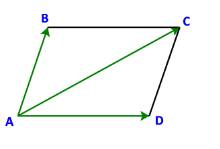
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:
a) \(\overrightarrow {DA} + \overrightarrow {DC} \)
b) \(\overrightarrow {AB} - \overrightarrow {AD} \)
c) \(\overrightarrow {OA} + \overrightarrow {OB} \) với O là giao điểm của AC và BD.
Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto \(\overrightarrow {CM} - \overrightarrow {NB} \).
Cho bốn điểm A, B, C, D. Chứng minh:
a) \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \)
b) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau.
Cho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai?
a) \(|\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |\)
b) \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB} \)
c) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \)
