a) 2x+y=4⇔y=−2x+4⇔x=12−y+2
. Do đó phương trình có nghiệm dạng tổng quát như sau:
{x∈Ry=−2x+4
hoặc {x=−12x+2y∈R
b) Vẽ (d1): 2x + y = 4
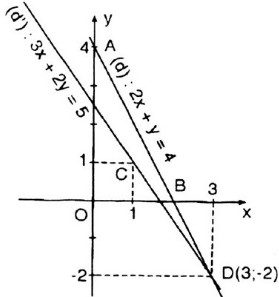
- Cho x = 0 => y = 4 được A(0; 4).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
- Cho x = 0 => y =  được C(0;
được C(0;  ).
).
- Cho y = 0 => x =  được D(
được D( ; 0).
; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.









