
Do hai đường tròn bằng nhau nên hai cung nhỏ AB bằng nhau. Vì cùng căng dây AB.
Suy ra  =
= 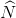 (cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B

Do hai đường tròn bằng nhau nên hai cung nhỏ AB bằng nhau. Vì cùng căng dây AB.
Suy ra  =
= 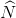 (cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
Cho 2 đường tròn (O) và (O’) cắt nhau tại 2 điểm A và B. Qua A vẽ dây cung AC của đường tròn (O) cắt (O’) tại C’. Qua B vẽ dây cung BD của đường tròn (O) cắt (O’) tại D’. AC và BD cắt nhau tại I. Chứng minh DC//D’C’.
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng. Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA. MB = MC.MD.
Cho hai đường tròn (O;R) và (O'R') (R>R')tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O') tại M cắt đường tròn (O) tại hai điểm B,C. Đường thẳng BO' cắt đường tròn (O) tại điểm thứ hai là D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC. Chứng minh rằng DF là phân giác của góc BDC.
Cho tam giác ABC nội tiếp (O) . Tia phân giác góc A cắt đường tròn tại M, tia phân giác góc ngoài tại đỉnh A cắt đường tròn tại N . CM:
a) tam giác MBC cân
b) CM: O, M, N thẳng hàng
Cho 2 đường tròn (O) và (O') cắt nhau tại A và B(O và O' nằm khác phía vs AB).Qua A kẻ cát tuyến cắt đường tròn (O) ở C.Cắt (O') ở D.Các tiếp tuyến của 2 đường tròn kẻ từ C và D,cắt nhau ở I.Chứng minh rằng khi cát tuyến CAD thay đổi thì:
a)Góc CBD ko đổi
b)Góc CID ko đổi
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.
Cho tam giác nhọn ABC nội tiếp đường tròn o . Các đường cao BD và CE của tam giác cắt nhau tại D. CM/ tứ giác ADCE và BCDE nội tieps đường tròn b.TIa BD và CE lần lượt cắt đường tròn tại M và N. Cm DE//MN c. ké đườn kính Ak. m tứ giác BKCM là hình thang cân
Cho đường tròn tâm O đường kính AB và S là một điểm nằm ngoài đường tròn. Vẽ đường thẳng SA và SB lần lượt cắt (O) tại điểm thứ hai M,N. Gọi H là giao điểm của AN và BM. Chứng minh rằng 1) SH ⊥ AB 2) HM . HB = HN . HA