Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Cho tứ giác ABCD có \(\widehat{A}=90^o;\widehat{D}=90^o\) . Góc A và góc D là hai góc đáy . Trên BC lấy điểm M là điểm nằm giữa sao cho MC=CD , MB= AB . Gọi giao điểm của AC và BD là N chứng minh MN\(\perp AD\)
Cho ΔABC vuông ở A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE ⊥ DC (E ∈ AC); DK ⊥ AC (K ∈ AC). Chứng minh BE // HK
Cho tam giác ABC có AB = 18 cm, AC = 12 cm, BC = 9 cm. Trên tia đối của tia CB lấy điểm D sao cho CD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AC tại E. Gọi F là giao điểm của AD và BE. Tính: a) Độ dài CE, DE
B1: Cho tam giác ABC có BC=3cm. Kéo dài BA lấy điểm D sao cho AD=2 lần AB. Kéo dài CA lấy điểm E sao cho AE =2 lần AC. Tính độ dài D B2: cho 2 tia Ax và By cố định so sánh cùng chiều điểm M di động trên tia Ax, điểm N di động trên tia By sao cho AM/BM= 1/2. Chứng minh đường thẳng MN đi qua 1 điểm cố định
cho tam giác ABC , AB= 10 cm , AC = 15cm , AM là trung tuyến. Trên AB lấy D sao cho AD = 4cm , trên AC lấy E sao cho CE = 9cm. gọi I là giao điểm DE và AM , cmr :
a) DE//BC
b) I là trung điểm DE
c) Gọi O là giao điểm của BE và CD , chứng minh A , O , M thẳng hàng
Cho tam giác ABC có cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N (h.5).
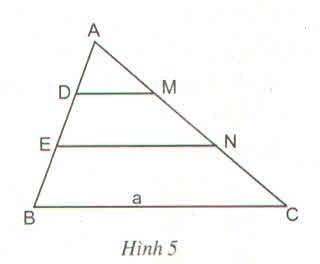
Tính theo a độ dài của các đoạn thẳng DM và EN ?
Cho tam giác ABC . Trên cạnh AC lấy hai điểm D, E sao cho ADDEEC . Trungtuyến AM cắt BD tại P và trung tuyến CN cắt BE tại Qa/ Chứng minh Q là trung điểm của CNb/ Chứng minh PQ // AC
Xem chi tiết
Cho góc xAy khác góc bẹt. Trên cạnh Ax lấy hai điểm B và D, trên cạnh Ay lấy hai điểm C và E sao cho AD/BD=11/8 và AC = 3/8 CE
a) CM: BC // DE
b) Biết BC = 3cm. Tính DE
Cho tam giác ABC có độ dài cạnh BC=a=15 cm . Trên cạnh lấy ba điểm D,E,F sao cho AD=DE=EF=FB. Trên cạnh AC lấy ba điểm M,N,P sao cho AM=MN=NP=PC . Tính độ dài các đoạn thẳng DM,EN,FP











