Tham khảo:
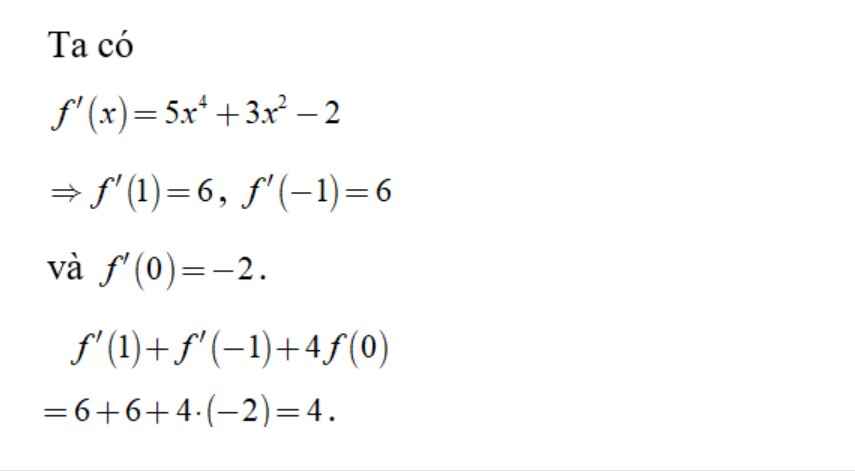
=>f'(1)+f'(-1)=-4f(0)
Tham khảo:
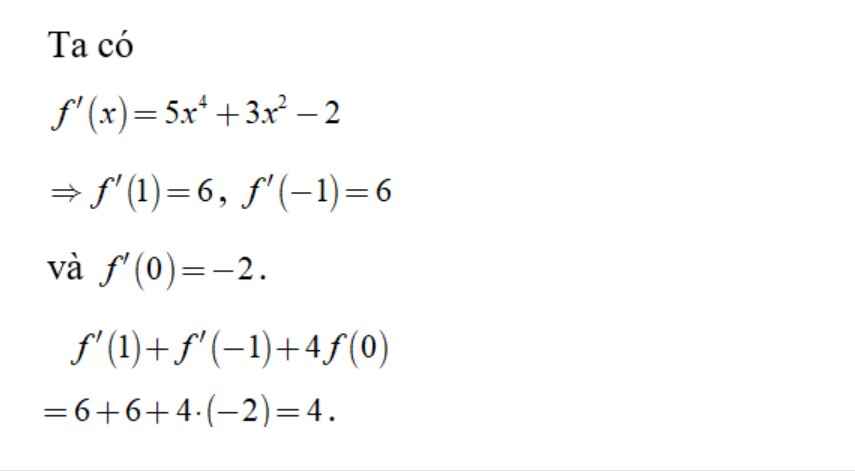
=>f'(1)+f'(-1)=-4f(0)
y=f(x) xác định có đạo hàm trên R thỏa mãn : \(\left[f\left(1+2x\right)\right]^2=x-\left[f\left(1-x\right)\right]^3\) . Viết phương trình tiếp tuyến tại điểm có hoành độ x =1 .
Cho \(f\left(x\right)=2x^3-x^2+\sqrt{3};g\left(x\right)=x^3+\dfrac{x^2}{2}-\sqrt{3}\)
Giải bất phương trình :
\(f'\left(x\right)>g'\left(x\right)\)
Giải các bất phương trình :
a) \(f'\left(x\right)>0\) với \(f\left(x\right)=\dfrac{1}{7}x^7-\dfrac{9}{4}x^4+8x-3\)
b) \(g'\left(x\right)\le0\) với \(g\left(x\right)=\dfrac{x^2-5x+4}{x-2}\)
c) \(\varphi'\left(x\right)< 0\) với \(\varphi\left(x\right)=\dfrac{2x-1}{x^2+1}\)
Xác định m để bất phương trình sau nghiệm đúng với mọi \(x\in R\)
a) \(f'\left(x\right)>0\) với \(f\left(x\right)=\dfrac{m}{3}x^3-3x^2+mx-5\)
b) \(g'\left(x\right)< 0\) với \(g\left(x\right)=\dfrac{m}{3}x^3-\dfrac{m}{2}x^2+\left(m+1\right)x-15\)
Cho \(f\left(x\right)=2x^3+x-\sqrt{2}\)
\(g\left(x\right)=3x^2+x+\sqrt{2}\)
Giải bất phương trình \(f'\left(x\right)>g'\left(x\right)\) ?
Rút gọn :
\(f\left(x\right)=\left(\dfrac{x-1}{2\left(\sqrt{x}+1\right)}+1\right)\left(\dfrac{2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x-2}}{\sqrt{x+2}+\sqrt{x-2}}+\dfrac{x+2}{\sqrt{x^2-4}-x+2}\right)\)
và tìm \(f'\left(x\right)\)
Tính \(f'\left(-1\right)\) biết \(f\left(x\right)=\dfrac{1}{x}+\dfrac{2}{x^2}+\dfrac{3}{x^3}\)
1. Cho hàm số \(y=x^3-3mx^2+3\left(2m-1\right)x+1\) . Với giá trị nào của m thì \(f'\left(x\right)-6x>0\) với mọi x>2
A. m > 1/2 B. m < -1/2 C. m >1 D. m ≤ 0
2. Cho hai hàm số f(x) và g(x) đều có đạo hàm trên R và thỏa mãn :
\(f^3\left(2-x\right)-2f^2\left(2+3x\right)+x^2g\left(x\right)+36x=0\) với mọi x thuộc R.
Tính \(A=3f\left(2\right)+4f'\left(2\right)\)
3. Biết hàm số f(x) - f(2x) có đạo hàm bằng 18 tại x=1 và đạo hàm bằng 2000 tại x=2. Tính đạo hàm của hàm số f(x) - f(4x) tại x=1
Cho \(f\left(x\right)=\dfrac{2}{x};g\left(x\right)=\dfrac{x^2}{2}-\dfrac{x^3}{3}\)
Giải bất phương trình :
\(f\left(x\right)\le g'\left(x\right)\)