Bài 8: Đường tròn nội tiếp. Đường tròn ngoại tiếp
Các câu hỏi tương tự
Cho (O; R) và một điểm A ở ngoài đường tròn . Từ A kẻ hai tiếp tuyến AP và AQ với (O) (P; Q là các tiếp điểm).Qua P kẻ đường thẳng song song với AQ cắt (O) tại M . Gọi N là giao điểm thứ hai của đường thẳng AM và đường tròn (O). 1) Cm tứ giác APOQ nội tiếp 2) Cm : AP2 AM . AN 3) Kẻ đường kính QS của đường tròn (O). Gọi H là giao điểm của NS và PQ, I là giao điểm của QS và MN. a) Cm NS là tia phân giác của góc PNM b) Cm HI // PM
Đọc tiếp
Cho (O; R) và một điểm A ở ngoài đường tròn . Từ A kẻ hai tiếp tuyến AP và AQ với (O) (P; Q là các tiếp điểm).Qua P kẻ đường thẳng song song với AQ cắt (O) tại M . Gọi N là giao điểm thứ hai của đường thẳng AM và đường tròn (O). 1) Cm tứ giác APOQ nội tiếp 2) Cm : AP2 = AM . AN 3) Kẻ đường kính QS của đường tròn (O). Gọi H là giao điểm của NS và PQ, I là giao điểm của QS và MN. a) Cm NS là tia phân giác của góc PNM b) Cm HI // PM
Cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA,SB của đường tròn (O;R) (với A,B là tiếp điểm). Đường thẳng a đi qua S (không đi qua tâm O) cắt đường tròn(O;R) tại hai điểm M,N (M nằm giữ S và N). a) CM: SO ⊥ AB b) Gọi I là trung điểm của MN và H là giao điểm của SO,AB ;hai đường...
Đọc tiếp
Cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA,SB của đường tròn (O;R) (với A,B là tiếp điểm). Đường thẳng a đi qua S (không đi qua tâm O) cắt đường tròn(O;R) tại hai điểm M,N (M nằm giữ S và N). a) CM: SO ⊥ AB b) Gọi I là trung điểm của MN và H là giao điểm của SO,AB ;hai đường thẳng OI và AB cắt nahu tại E.CM: OI.OE=R2 (vẽ hộ em hình luôn ạ)
Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB với đường tròn (O). Qua điểm M kẻ cát tuyến MCD với đường tròn (O), tức là đường thẳng đi qua điểm M và cắt đường tròn tại hai điểm là C, D). Gọi I là trung điểm của dây CD, Khi đó MAOIB có là ngũ giác nội tiếp hay không ?
cho tam giác abc có 3 góc nhọn ( AB AC) nội tiếp đường tròn tâm o. kẻ đường thẳng d là tiếp tuyến tại A của đường tròn tâm o . Gọi d là đường thẳng đi qua B và song song với d; d cắt các đường thẳng Ao , AC lần lượt tại E, D. Kẻ À là đường cao của tam giác ABC ( F thuộc BC ) a) Chướng minh rằng tứ giác ABFE nội tiếp b) chướng minh rằng AB2 AD * ACc) Gọi M,N lần lượt là trung diểm của AB, BC . CMR: MN vuông góc với EFGiúp mình với
Đọc tiếp
cho tam giác abc có 3 góc nhọn ( AB < AC) nội tiếp đường tròn tâm o. kẻ đường thẳng d là tiếp tuyến tại A của đường tròn tâm o . Gọi d' là đường thẳng đi qua B và song song với d; d' cắt các đường thẳng Ao , AC lần lượt tại E, D. Kẻ À là đường cao của tam giác ABC ( F thuộc BC )
a) Chướng minh rằng tứ giác ABFE nội tiếp
b) chướng minh rằng AB2 = AD * AC
c) Gọi M,N lần lượt là trung diểm của AB, BC . CMR: MN vuông góc với EF
Giúp mình với
Cho tam giác ABC cân tại B có AB < AC nội tiếp trong đường tròn (O). Gọi (d) là tiếp tuyến với đường tròn tại điểm A. Một đường thẳng song song với (d) cắt các cạnh AB, AC và đường thẳng BC lần lượt tại D, E và I. a) Chứng minh rằng số do hai cung nhỏ BA và BC bằng nhau. b) Chứng minh rằng góc ABC = AED. c) Chứng minh tứ giác BCED nội tiếp. d) Chứng minh rằng IB.IC =
trên đường tròn O lấy ba điểm A,B,C sao cho tam giác ABC nhọn. gọi AD,BE,CF là các đường cao của tam giác ABC; Đường thẳng EF cắt BC tại P.Qua D kẻ đường thẳng song song với đường thẳng EF cắt đường thẳng AC và AB lần lượt tại Q và R, M là trung điểm của BC.
a, CM tứ giác BQCR là tứ giác nội tiếp
b, CM hai tam giác EPM và DEM đồng dạng
Cho đường tròn (O; R) , dây AB cố định (AB không đi qua O). I là trung điểm của AB. Trên cung lớn AB lấy 1 điểm C. Các đường cao AD, BE cắt nhau tại H và cắt đường tròn tại điểm thứ hai lần lượt ở M và N. Gọi K là trung điểm của CH. Chứng minh:a) Tứ giác ABDE nội tiếpb) MN // DE.c) Đoạn thẳng CK có độ dài không đổi khi C di chuyển trên cung lớn AB.
Đọc tiếp
Cho đường tròn (O; R) , dây AB cố định (AB không đi qua O). I là trung điểm của AB. Trên cung lớn AB lấy 1 điểm C. Các đường cao AD, BE cắt nhau tại H và cắt đường tròn tại điểm thứ hai lần lượt ở M và N. Gọi K là trung điểm của CH. Chứng minh:
a) Tứ giác ABDE nội tiếp
b) MN // DE.
c) Đoạn thẳng CK có độ dài không đổi khi C di chuyển trên cung lớn AB.
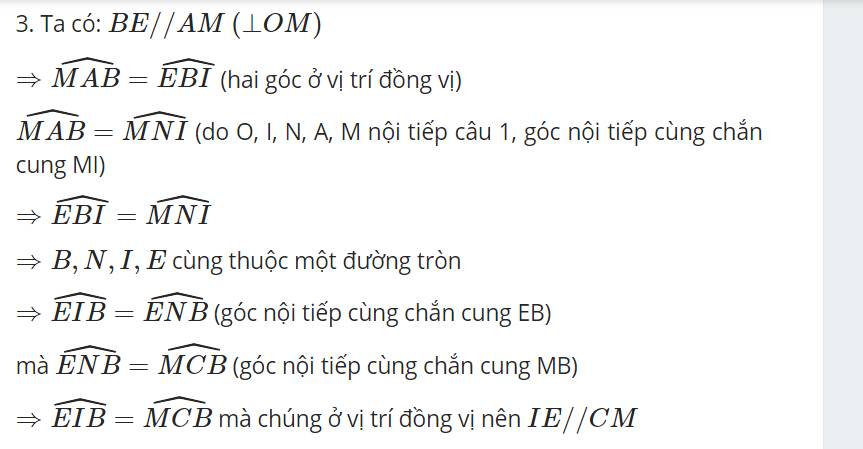
Cho đường tròn ( O : R) và điểm A nằm cố định bên ngoài đường tròn .Qua A vẽ cát tuyến ABC với đường tròn (B nằm giữa A và C ), AM , AN là các tiếp tuyến với O , gọi H là trung điểm của BC.
a,chứng minh AM^2 AB.AC
b, chứng minh tứ giác AHMN nội tiếp
c, đường thẳng B song song với AM cắt MN tại E. Chứng minh rằng EH // MC .
d, Khi cát tuyến ABC quay quanh Atì trọng tâm tam giácMBC chuyển động trên đường nào
Đọc tiếp
Cho đường tròn ( O : R) và điểm A nằm cố định bên ngoài đường tròn .Qua A vẽ cát tuyến ABC với đường tròn (B nằm giữa A và C ), AM , AN là các tiếp tuyến với O , gọi H là trung điểm của BC.
a,chứng minh AM^2 = AB.AC
b, chứng minh tứ giác AHMN nội tiếp
c, đường thẳng B song song với AM cắt MN tại E. Chứng minh rằng EH // MC .
d, Khi cát tuyến ABC quay quanh Atì trọng tâm tam giácMBC chuyển động trên đường nào
cho góc XOY và một đường tròn tâm I tiếp xúc với 2 cạnh của góc tại A và B . Qua A kẻ đường thẳng vuông góc với OB , cắt đường tròn tại điểm C . Gọi K là trung điểm của đoạn thẳng OB , đương thẳng AK cắt đường tròn tại E.
a) CM OAIB nội tiếp
b) CM KO(bình phương) = KA.KE