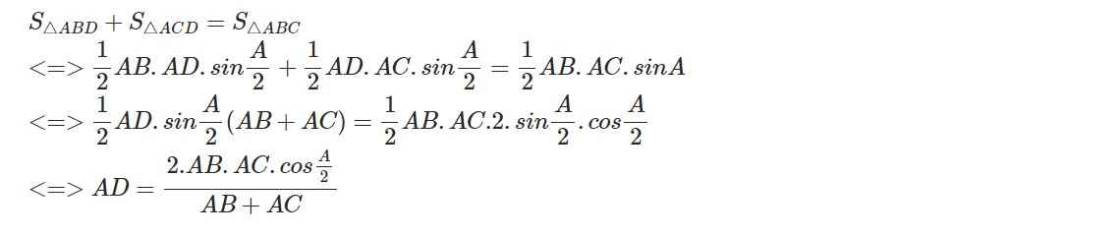
=>\(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{\sqrt{2}}{AD}\)
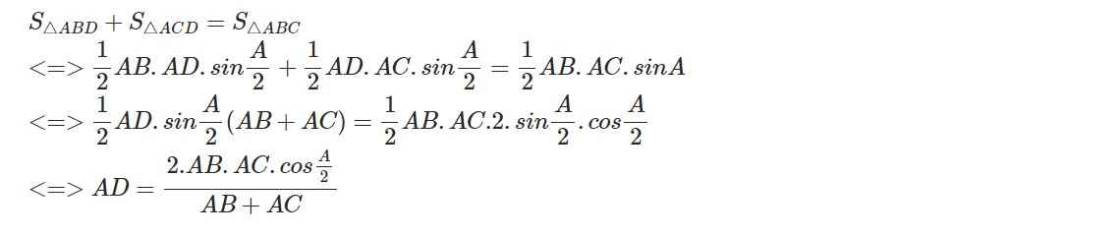
=>\(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{\sqrt{2}}{AD}\)
Cho \(\Delta\)ABC vuông tại A, đường cao AH.
a. CMR: \(\Delta\)ABC đồng dạng \(\Delta\)HBA. suy ra: AB2=BH.BC
b. Trên tia đối của tia AC lấy điểm D sao AD<AC. vễ đường thẳng đi qua H song song với AC cắt Ã, BD lần lượt tại M, N.
CMR: \(\dfrac{MN}{MH}=\dfrac{AD}{AC}\)
C. Vẽ AE\(\perp\)BD tại E. CMR: \(\widehat{BEH}=\widehat{BAH}\)
Cho tam giác ABC vuông tại A ( AC>AB), đường cao AH \(\left(H\in BC\right)\).Trên tia HC lấy điểm D sao cho HD=HA . Đường vuông góc với BC tại D cắt AC tại E .Gọi M là trung điểm của đoạn thẳng BE.
a, Chứng minh rằng \(BE=\sqrt{2}AB\) và \(\Delta BHM\approx\Delta BEC\)
b, Tia AM cắt BC tại G . Chứng minh :\(\dfrac{GB}{BC}=\dfrac{HD}{AH+HC}\)
Cho tam giác ABC, góc A = 90 độ, kẻ AH vuông góc BC tại H. Chứng minh:
\(AH^2=HB.HC\)
\(AB^2=HB.BC\)
\(AC^2=HC.BC\)
\(\dfrac{1}{AH^2}=\dfrac{1}{BA^2}+\dfrac{1}{AC^2}\)
Cho ΔABC, các đường phân giác BD, CE, AK cắt nhau tại I.
Biết AB = 4cm, AC = 5cm, BC = 6cm.
a) Tính tỉ số: \(\dfrac{AD}{AC}\); \(\dfrac{BE}{BA}\); \(\dfrac{DI}{DB}\)
b) Tính tỉ số diện tích ΔDIE và ΔABC
c) Chứng minh rằng: \(\dfrac{KI}{AK}\) + \(\dfrac{ID}{BD}\) + \(\dfrac{EI}{EC}\) = 1
Bài 1; cho ΔABC vuông tại A.trong đó AB=8cm; AC=6cm; AD là tia phân giác của góc A(D∈BC)
a) Tính tỉ số DB/DC
b) Kẻ đường cao AH (H∈BC) CMR: ΔAHB đồng dạng với ΔCHA và AB2/BH=AC2/CH
Cho \(\Delta ABC\) cố định, các điểm D và E di đoonhj trên các cạnh tương ứng là AB và AC sao cho \(\dfrac{AD}{DB}=\dfrac{CE}{EA}\)
CMR: Trung điểm M của đoạn thẳng DE nằm trên 1 đoạn thẳng cố định
Cho tam giác ABC có ba góc nhọn. Các đường cao AM, BN, CK cắt nhau tại H (M ∈ BC, N ∈ AC, K ∈ AB). Gọi A1, B1, C1 lần lượt là điểm đối xứng với H qua BC, AC, AB. Chứng minh rằng:
a) ΔBHK đồng dạng với ΔCHN.
b) ΔKHN đồng dạng với ΔBHC.
c) BH.BN + CH.CK = BC2.
d) Tổng \(\dfrac{AA_1}{AM}+\dfrac{BB_1}{BN}+\dfrac{CC_1}{CK}\) có giá trị không đổi.
27.Cho tam giác ABC vuông tại A , kẻ AH vuông góc với BC (H thuộc BC). CMR
a) AH.BC=AB.AC
b) AB2 =BH.BC
c) AC2 =CH.BC
d)\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
Cho tam giác ABC vuông tại A , có AB = 3cm , AC = 4cm. Kẻ đường phân giác BD của góc ABC( D ∈ AC).
a) Tính BC, AD, DC
b) TRên BC lấy điểm E sao cho CE = 2cm. Chứng minh ΔCED ∼ΔCAB
c) Chứng minh ED= AD