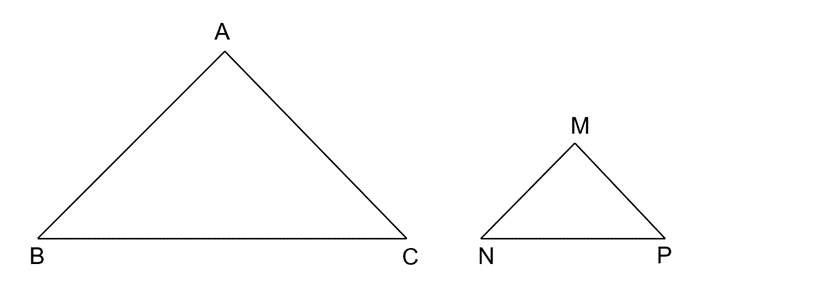
a) Tam giác ABC tại A nên \(\widehat B = \widehat C\) (1)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (2)
Từ (1) và (2) nên \(\widehat N = \widehat P\) suy ra tam giác MNP cân tại M.
b) Vì tam giác ABC là tam giác đều nên \(\widehat A = \widehat B = \widehat C = {60^o}\)(3)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (4)
Từ (3) và (4) suy ra \(\widehat M = \widehat N = \widehat P = {60^o}\) nên tam giác MNP là tam giác đều.
c) Vì tam giác ABC có \(AB \ge AC \ge BC\) suy ra \(\widehat C \ge \widehat B \ge \widehat A\) (quan hệ giữa góc và cạnh đối điện) (5)
Mà \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (6)
Từ (5) và (6) suy ra \(\widehat P \ge \widehat N \ge \widehat M\) nên \(MN \ge MP \ge NP\)