Question

cho ΔABC vuông cân tại A, AC = 4cm. Điểm M thuộc cạnh BC. Gọi D và E là chân các đường vuông góc kẻ từ M đến AB, AC
a) ADME là hình gì ? tính chu vi tứ giác đó
b) Điểm M ở vị trí nào trên cạnh BC thì đoạn thẳng DE có độ dài nhỏ nhất

Answer 1

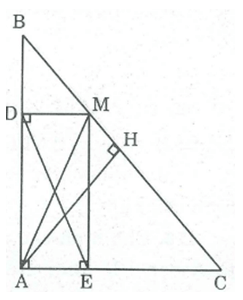
a. Xét tứ giác ADME ta có:

MD ⊥ AB (gt)

ME ⊥ AC (gt)

Suy ra: Tứ giác ADME là hình chữ nhật (vì có ba góc vuông)

∆ ABC vuông cân tại A

Suy ra: ∆ DBM vuông cân tại D ⇒ DM = DB

Chu vi hình chữ nhật ADME bằng :

2(AD + DM) = 2 ( AD + DB) = 2 AB = 2.4 = 8 (cm)

b. Gọi H là trung điểm của BC

Suy ra: AH ⊥ BC (tính chất tam giác cân)

AM ≥ AH (dấu “=” xảy ra khi M trùng với H)

Tứ giác ADME là hình chữ nhật

⇒ AM = DE (tính chất hình chữ nhật)

Suy ra: DE ≥ AH

Vậy DE = AH có độ dài nhỏ nhất khi điểm M là trung điểm của BC.

Answer 2

0 là độ nha hơi lộn mấy chỗ

Answer 3

Chúc bạn học tốt!