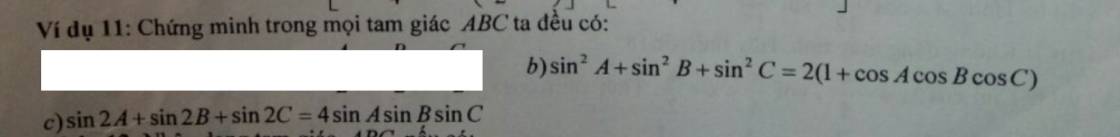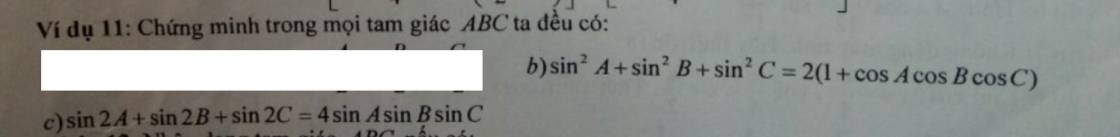b)
Trong tam giác ABC có:
`sin^2(A) = 1 - cos^2(A) = 1 - (2sin(A/2)cos(A/2))^2 = 1 - 4sin^2(A/2)cos^2(A/2) = 1 - 4sin^2(A/2)(1 - sin^2(A/2)) = 4sin^2(A/2)sin^2(B/2)sin^2(C/2)`
Với R là bán kính đường tròn ngoại tiếp tam giác ABC và r là bán kính đường tròn nội tiếp tam giác ABC:
`sin^2(A) = 4sin^2(A/2)sin^2(B/2)sin^2(C/2) = 4(1/8R/r)^2 = 1/2^2R^2/r^2 = 1/4R^2/r^2`
Với a, b, c là độ dài các cạnh tam giác ABC và S là diện tích tam giác ABC:
`sin^2(A) = 1/4R^2/r^2 = 1/4(abc / 4S)^2/r^2 = abc^2 / 16S^2r^2`
Với r là bán kính đường tròn nội tiếp tam giác ABC:
`sin^2(A) = abc^2 / 16S^2r^2 = abc^2 / 16[(a + b + c)r / 2]^2r^2 = abc^2 / 16(a + b + c)^2r^3`
Áp dụng tương tự với `sin^2B` và `sin^2C`
Tổng các biểu thức trên:
`sin^2(A) + sin^2(B) + sin^2(C) = abc^2 / 16(a + b + c)^2r^3 + bca^2 / 16(b + c + a)^2r^3 + cab^2 / 16(c + a + b)^2r^3
= (abc^2 + bca^2 + cab^2) / 16(a + b + c)^2r^3
= 4sin(A)sin(B)sin(C)`