a: Xét ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
Diện tích tam giác ABC là: \(S_{ABC}=\frac12\cdot AB\cdot AC=\frac12\cdot9\cdot12=6\cdot9=54\left(\operatorname{cm}^2\right)\)
Ta có: M là trung điểm của OB
=>\(BM=\frac12BO=\frac12\cdot\frac12\cdot BC=\frac14BC\)
=>\(S_{ABM}=\frac14\cdot S_{ABC}=\frac{54}{4}=13,5\left(\operatorname{cm}^2\right)\)
b: Xét ΔBOI vuông tại O và ΔBAC vuông tại A có
\(\hat{OBI}\) chung
Do đó: ΔBOI~ΔBAC
=>\(\frac{BO}{BA}=\frac{BI}{BC}\)
=>\(\frac{BO}{BI}=\frac{BA}{BC}\)
Xét ΔBOA và ΔBIC có
\(\frac{BO}{BI}=\frac{BA}{BC}\)
góc OBA chung
Do đó: ΔBOA~ΔBIC
c: Ta có: \(\frac{BO}{BI}=\frac{BA}{BC}\)
=>\(BA\cdot BI=BO\cdot BC\)
=>\(BA\cdot BI=2\cdot BM\cdot\frac12\cdot BN=BM\cdot BN\)
=>\(\frac{BA}{BN}=\frac{BM}{BI}\)
Xét ΔBAM và ΔBNI có
\(\frac{BA}{BN}=\frac{BM}{BI}\)
góc ABM chung
Do đó: ΔBAM~ΔBNI
=>\(\frac{S_{BAM}}{S_{BNI}}=\left(\frac{BA}{BN}\right)^2=\left(\frac{BA}{2\cdot BC}\right)^2=\left(\frac{9}{2\cdot15}\right)^2=\left(\frac{9}{30}\right)^2=\frac{9}{100}\)
=>\(\frac{13.5}{S_{BNI}}=\frac{9}{100}=\frac{13.5}{150}\)
=>\(S_{BNI}=150\left(\operatorname{cm}^2\right)\)












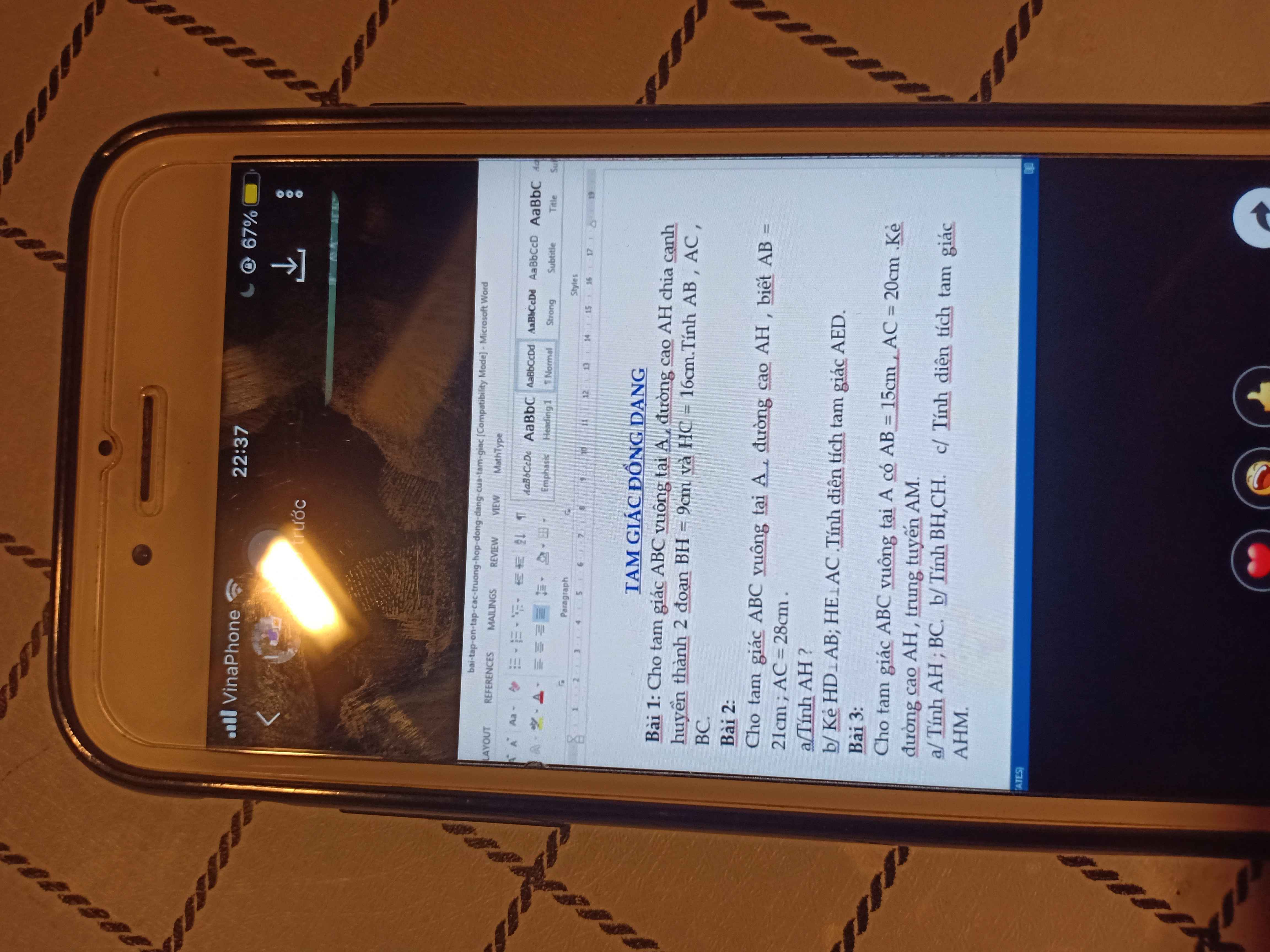

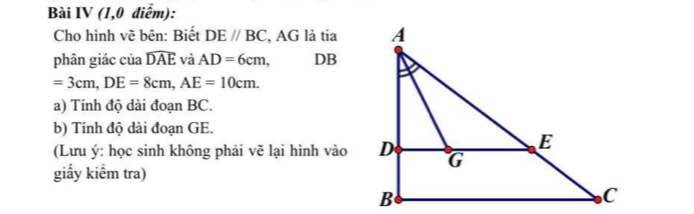



 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ

