a)
có `AB=AD+DB=6+3=9(cm)`
xét tam giác ABC có DE//BC(gt)
`=>(AD)/(AB)=(DE)/(BC)` (định lí talet)
`=>6/9=8/(BC)`
`=>BC=12` (cm)
b)
xét tam giác ADE có AG là phân giác góc DAE (gt)
`=>(AD)/(AE)=(GD)/(GE)` (tính chất đường phân giác)
`=>6/10=(GD)/(GE)`
`=>3/5=(GD)/(GE)`
`=>(GD)/3=(GE)/5`
Mà `DE=GD+GE=8cm`
áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{GD}{3}=\dfrac{GE}{5}=\dfrac{GD+GE}{3+5}=\dfrac{8}{8}=1\)
`=>GE=1*5=5(cm)`
a: Xet ΔACB có
DE//BC
=>AD/AB=DE/BC
=>8/BC=6/9=2/3
=>BC=12cm
b: Xet ΔADE có AG la phân giác
nên GD/AD=GE/AE
=>GD/3=GE/5=(GD+GE)/(3+5)=8/8=1
=>GE=5cm

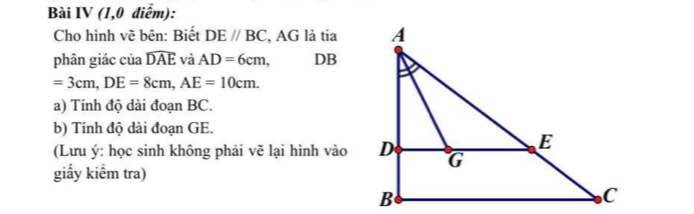






 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ