Ôn tập: Phân thức đại số
Các câu hỏi tương tự
cho biểu thức: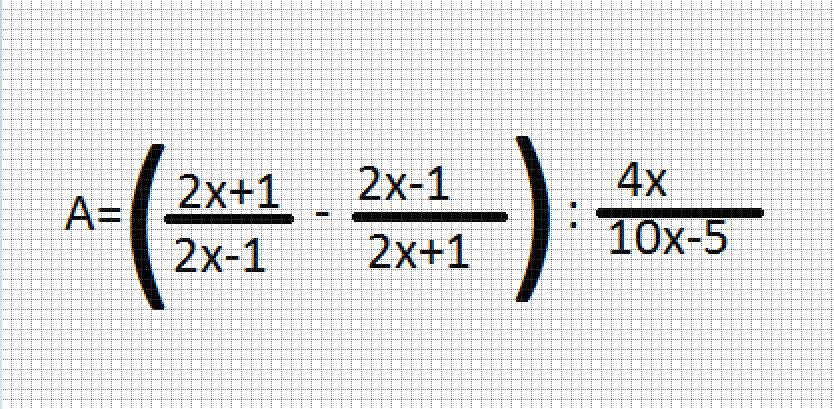
a)tìm điều kiện của x để giá trị của biểu thức A được xác định
b)rút gọn biểu thức
cho biểu thức P=\(\dfrac{3x^2+6x+12}{x^3-8}\)
a) Tìm ĐKXĐ của P
b) Rút gọn biểu thức P
c) Tính giá trị của P với x=\(\dfrac{4001}{2000}\)
Cho hai biểu thức:
A dfrac{x+6}{5-x} và B dfrac{x+5}{2x}+dfrac{x-6}{x-5}+dfrac{x^2-8x-25}{2x^2-10x}
a) Tính giá trị biểu thức A với x thỏa mãn x^2+5x0
b) Chứng minh: B dfrac{x-2}{x-5}
c) Tìm giá trị của x để B-A0
d) Tìm tất cả giá trị nguyên của x để biểu thức A có giá trị nguyên.
Đọc tiếp
Cho hai biểu thức:
A = \(\dfrac{x+6}{5-x}\) và B = \(\dfrac{x+5}{2x}+\dfrac{x-6}{x-5}+\dfrac{x^2-8x-25}{2x^2-10x}\)
a) Tính giá trị biểu thức A với x thỏa mãn \(x^2+5x=0\)
b) Chứng minh: B = \(\dfrac{x-2}{x-5}\)
c) Tìm giá trị của x để \(B-A=0\)
d) Tìm tất cả giá trị nguyên của x để biểu thức A có giá trị nguyên.
1) Dùng định nghĩa 2 phân thức bằng nhau chứng tỏ rằng
frac{3-x}{3+x} frac{x^2-6x+9}{9-x^2}
Rút gọn phân thức sau
frac{54left(x-3right)^3}{63left(3-xright)^2}
Tìm giá trị của x để biểu thức có giá trị nhỏ nhất, giá trị lớn nhất:
a) giá trị lớn nhất
A frac{2x^2+12x+24}{x^2+6x+11}
b) giá trị nhỏ nhất
B frac{x^2+4x+5}{x^2+4x+7}
Đọc tiếp
1) Dùng định nghĩa 2 phân thức bằng nhau chứng tỏ rằng
\(\frac{3-x}{3+x}\) = \(\frac{x^2-6x+9}{9-x^2}\)
Rút gọn phân thức sau
\(\frac{54\left(x-3\right)^3}{63\left(3-x\right)^2}\)
Tìm giá trị của x để biểu thức có giá trị nhỏ nhất, giá trị lớn nhất:
a) giá trị lớn nhất
A= \(\frac{2x^2+12x+24}{x^2+6x+11}\)
b) giá trị nhỏ nhất
B= \(\frac{x^2+4x+5}{x^2+4x+7}\)
Chú ý rằng vì left(x+aright)^2ge0 với mọi giá trị của x và left(x+aright)^20 khi x-a nên left(x+aright)^2+bge b với mọi giá trị của x và left(x+aright)^2+bb khi x-a. Do đó giá trị nhỏ nhất của left(x+aright)^2+b bằng b khi x-a.
Áp dụng điều này giải các bài tập sau :
a) Rút gọn rồi tìm giá trị của x để biểu thức :
dfrac{x^2}{x-2}left(dfrac{x^2+4}{x}-4right)+3 có giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy ?
b) Rút gọn rồi tìm giá trị của x để biểu thức:
dfrac{lef...
Đọc tiếp
Chú ý rằng vì \(\left(x+a\right)^2\ge0\) với mọi giá trị của x và \(\left(x+a\right)^2=0\) khi \(x=-a\) nên \(\left(x+a\right)^2+b\ge b\) với mọi giá trị của x và \(\left(x+a\right)^2+b=b\) khi \(x=-a\). Do đó giá trị nhỏ nhất của \(\left(x+a\right)^2+b\) bằng b khi \(x=-a\).
Áp dụng điều này giải các bài tập sau :
a) Rút gọn rồi tìm giá trị của x để biểu thức :
\(\dfrac{x^2}{x-2}\left(\dfrac{x^2+4}{x}-4\right)+3\) có giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy ?
b) Rút gọn rồi tìm giá trị của x để biểu thức:
\(\dfrac{\left(x+2\right)^2}{x}\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\) có giá trị lớn nhất. Tìm giá lớn nhất ấy ?
Tính giá trị nhỏ nhất của các biểu thức sau:
a) A = 4x2 +4x + 11
b) C = x2 - 2x + y2 - 4y + 7
Cho biểu thức
\(A=\dfrac{x+1}{x-2}+\dfrac{x-1}{x+2}+\dfrac{x^2+4x}{4-x^2}\left(x\ne\pm2\right)\)
a) Rút gọn A
b) Tính giá trị của biểu thức A khi x = 4
c) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên dương
cho biểu thức P= \(\frac{8x^3-12x^2+6x-1}{4x^2-4x+1}\)
a) Tìm điều kiện xác định của biểu thức P
b) Rút gọn P
c) Chứng minh rằng với mọi giá trị của x nguyên thì P nguyên
tìm giá trị lớn nhất và nhỏ nhất của biểu thức B=x+y+z biết rằng x,y,z là các số thỏa mãn điều kiện y^2+yz+z^2= 2- 3x^2/2















