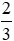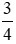Ta có: \(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{50}< \dfrac{1}{60}\times30\)
\(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{50}< \dfrac{1}{2}< \dfrac{3}{4}\)(đpcm)
Lời giải:
$\frac{1}{21}+\frac{1}{22}+...+\frac{1}{30}> \frac{1}{30}+\frac{1}{30}+...+\frac{1}{30}=\frac{10}{30}=\frac{1}{3}$
$\frac{1}{31}+\frac{1}{32}+...+\frac{1}{40}> \frac{10}{40}=\frac{1}{4}$
$\frac{1}{41}+\frac{1}{42}+....+\frac{1}{50}> \frac{10}{50}=\frac{1}{5}$
Cộng lại:
$A> \frac{1}{3}+\frac{1}{4}+\frac{1}{5}$
$A> \frac{47}{60}> \frac{3}{4}$