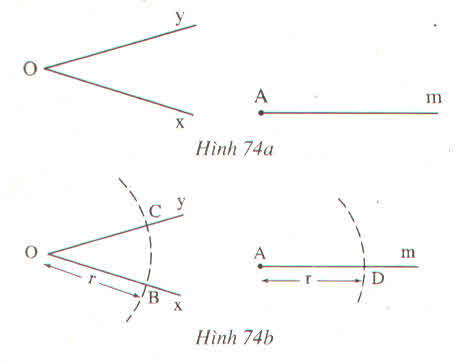
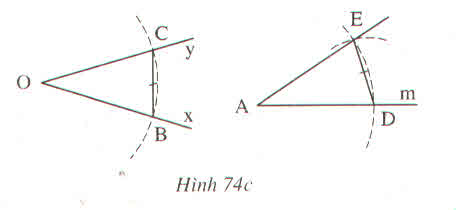
∆BAC và ∆BAD có: AC= AD (gt)
BC = BD(gt) AB cạnh chung.
Nên ∆BAC= ∆BAD(c.c.c)
Suy ra ∠BAC = ∠BAD (góc tương ứng)
Vậy AB là tia phân giác của góc CAD

Vì đường tròn tâm A cắt đường tròn tâm B tại C và D nên C và D thuộc đường tròn tâm A và đường tròn tâm B
Vì C và D thuộc đường tròn tâm A nên
Ta có AC=AD
Vì C và D thuộc đường tròn tâm B nên
Ta có BC=BD
Xét tam giác ABC và tam giác ABD có
+ AC=AD (cmt)
+ BC=BD(cmt)
+ AB là cạnh chung
Do đó tam giác ABC bằng tam giác ABD
Từ đó Suy ra được
Góc CAB bằng góc DAB (hai góc tương ứng)
Vậy AB là tia phân giác góc CAD (đpcm)
Chúc bạn học tốt môn Toán ![]() Mình chắc chắn đúng 100%. Cô mình dạy rồi!!!!!!!!!
Mình chắc chắn đúng 100%. Cô mình dạy rồi!!!!!!!!!
Nhân tiện nếu mình làm đúng, bạn dễ hiểu thì tick cho mình nha ![]()