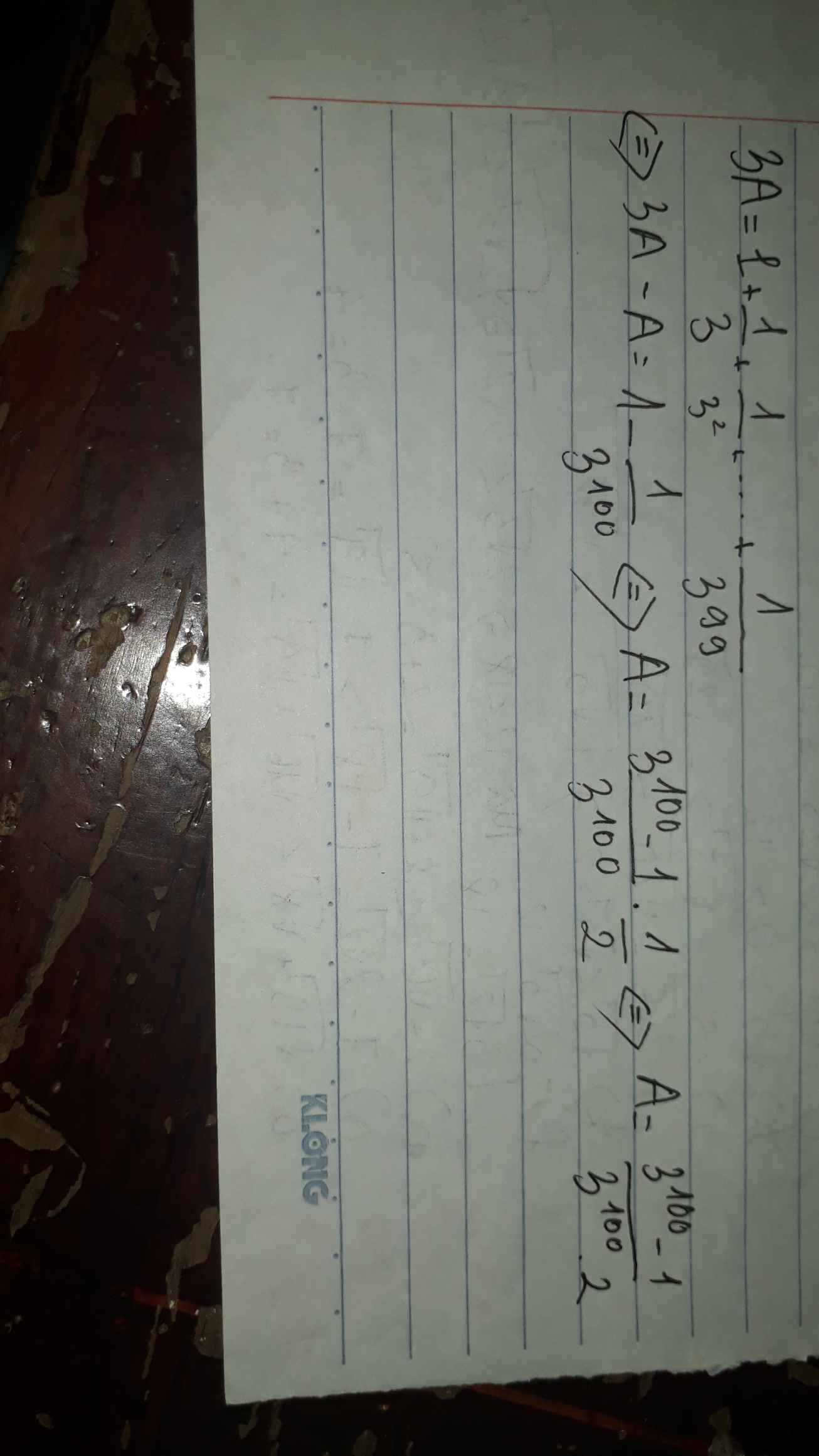Question

Bài 1: Tính tổng

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\)

 

Answer 1

Answer 2

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\\ \Leftrightarrow3A=3\left(+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\\ =1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)

Lấy 3A - A ta được
\(3A-A=\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\\ 2A=1-\dfrac{1}{3^{100}}\\ \Leftrightarrow A=\dfrac{1-\dfrac{1}{3^{100}}}{2}\)

Answer 3

Ta có: \(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\)

\(\Leftrightarrow3A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)

\(\Leftrightarrow2\cdot A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{100}}\)

\(\Leftrightarrow2\cdot A=1-\dfrac{1}{3^{100}}\)

\(\Leftrightarrow2\cdot A=\dfrac{3^{100}-1}{3^{100}}\)

\(\Leftrightarrow A=\dfrac{3^{100}-1}{2\cdot3^{100}}\)