Question

Ba điện trở R₁= 6Ω, R₂= 8Ω và R₃ mắc song song giữa hai điểm A, B có hiệu điện thế U= 24V. Cường độ dòng điện chính I= 9A.

A) tính I₁, I₂, I₃ và R₃.

B) tính điện trở tương đương của đoạn mạch.

Answer 1

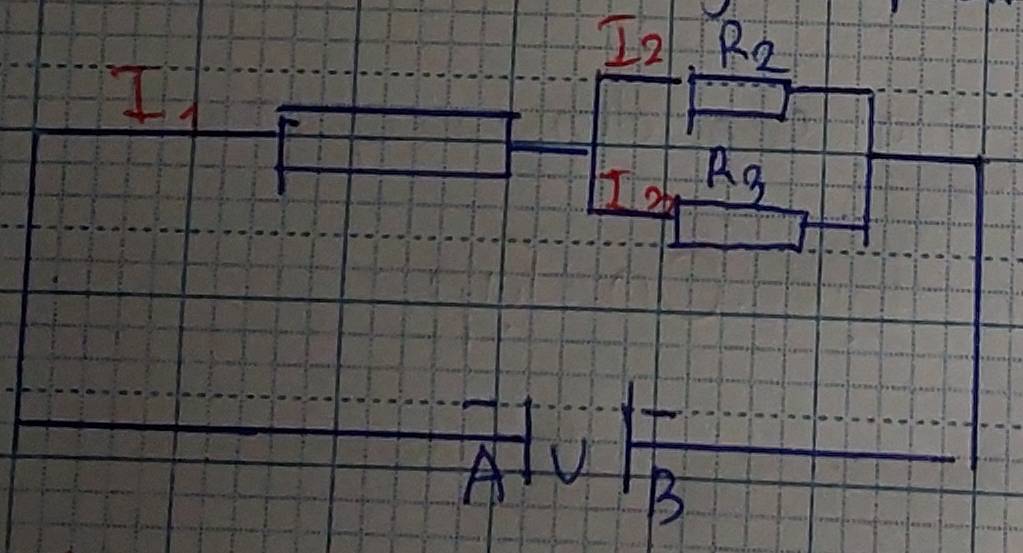
a) Vì \(R_1\text{/}\text{/}R_2\text{/}\text{/}R_3\) nên: \(U=U_1=U_2=U_3\)

\(\Rightarrow\left\{{}\begin{matrix}I_1=\dfrac{U}{R_1}=\dfrac{24}{6}=4\left(A\right)\\I_2=\dfrac{U}{R_2}=\dfrac{24}{8}=3\left(A\right)\end{matrix}\right.\)

Vì \(R_1\text{/}\text{/}R_2\text{/}\text{/}R_3\) nên: \(I=I_1+I_2+I_3\)

\(\Rightarrow I_3=I-I_1-I_2=9-3-4=2\left(A\right)\)

\(\Rightarrow R_3=\dfrac{U}{I_3}=\dfrac{24}{2}=12\left(\Omega\right)\)

b) Điện trở tương đương của đoạn mạch là:

\(R_{TĐ}=\dfrac{U}{I}=\dfrac{24}{9}\approx2,667\left(\Omega\right)\)

Vậy .......................

Answer 2

a. Phân tích mạch: R1//R2//R3

+.Do R1//R2//R3 \(\Rightarrow\) I1= \(\dfrac{U}{R1}\) = \(\dfrac{24}{6}\)=4A (U=U1=U2)

I2=\(\dfrac{U}{R2}\)=\(\dfrac{24}{8}\)=3A (U=U1=U2)

I3=I-(I1+I2)=9-(4+3)=2A

+. R3=\(\dfrac{U}{I3}\)=\(\dfrac{24}{2}\)=12Ω

b.Vì R1//R2//R3\(\Rightarrow\)

Rtđ=\(\dfrac{R1.R2.R3}{R1+R2+R3}\)=\(\dfrac{6.8.12}{6+8+12}\)=\(\approx22\)