Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho dfrac{AE}{ED}dfrac{p}{q}. Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
Chứng minh rằng :
EFdfrac{p.CD+q.AB}{p+q}
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Đọc tiếp
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho \(\dfrac{AE}{ED}=\dfrac{p}{q}\). Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
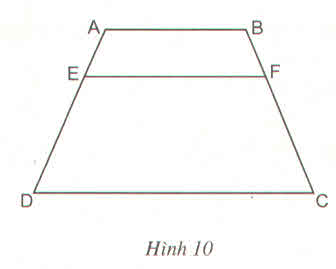
Chứng minh rằng :
\(EF=\dfrac{p.CD+q.AB}{p+q}\)
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Cho DABC vuông tại A, đường phân giác của góc A cắt BC tại D biết AB = 6 cm , AC = 8 cm . a) Tính BC, BD, DC b) Từ trung điểm M của BC kẻ 1 đường thẳng song song với AD cắt cạnh AC tại F và cắt tia đối của tia AB tại E .Chứng minh: . c) Chứng minh: AE = AF
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H (h.16)
a) Chứng minh rằng :
dfrac{AH}{AH}dfrac{BC}{BC}
b) Áp dụng : Cho biết AHdfrac{1}{3}AH và diện tích tam giác ABC là 67,5cm^2. Tính diện tích tam giác ABC ?
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16)
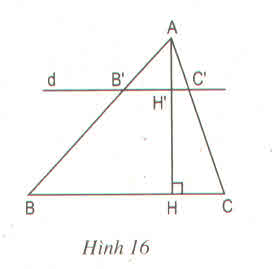
a) Chứng minh rằng :
\(\dfrac{AH'}{AH}=\dfrac{B'C'}{BC}\)
b) Áp dụng : Cho biết \(AH'=\dfrac{1}{3}AH\) và diện tích tam giác ABC là \(67,5cm^2\). Tính diện tích tam giác AB'C' ?
Cho tam giác ABC,các đường tung tuyến BM,CN cắt nhau tại G, K là giao điểm trên cạnh BC. Đường thẳng qua K song song với CN cắt AB tại D, đường thẳng qua K song song với BM cắt AC tại E. Gọi I là giao điểm của KG và DE. Chứng minh rằng I là trung điểm của DE
Mong mấy anh chị giúp giùm em!Em cảm ơn trước.
Help tui với cần gấp!!!! Cho ∆ABC,đường cao AH trên cạnh AB lấy M sao cho AB=3AM.Qua M kẻ đường thẳng vuông góc với AH tại K cắt AC tại N. 1)CM:AK=1/3 AH 2)CM:AM.AC=AN.AB 3)Cho biết S(ABC) gấp mấy lần S(AMN)? Áp dụng định lí đảo Ta lét và hệ quả của định lí ta lét.
Bài 6: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK, M thuộc AC, kẻ KN song song với CI, N thuộc AB.
a) Chứng minh MN song song với BC.
b) Gọi E là trung điểm của BC, F là giao điểm của BK và AE, H là giao điểm của CF và AB. Chứng minh HK song song với BC.
Cho tam giác ABC vuông tại A, trên tia đối của AB lấy điểm D, một đường thẳng qua D song song với BC cắt đường thẳng AC tại E. Tính các cạnh AD, AE của tam giác ADE biết AB=3cm, AC=4cm, DE=10cm
Cho Tam giác KIM vuông tại K, đường phân giác của góc K cắt IM tại B. a. Tính IM, BI, BM biết KI = 15cm , KM = 20cm . b. Từ trung điểm A của IM kẻ đường thẳng song song với KB cắt cạnh KM tại C và tia IK tại H. Chứng minh: (MA)/(MB) = (AC)/(KB) c. Chứng minh: Tam giác KHC cân và H = MC d. Kẻ các đường phân giác ID và MN của tam giác KIM . Chứng minh : BI/BM * DM/DK * NK/NI =1
BT1: Cho tam giác ABC, trung tuyến AM.Lấy điểm N trên cạnh AB, điểm Q trên cạnh AC sao cho NQ// BC. Gọi K là giao của AM và NQ. Cmr: NK=KQ.
BT2: Cho hình bình hành ABCD, trên tia đối của tia CB lấy điểm I, AI cắt BD,
DC lần lượt ở K,G. Chứng minh:
a, CI/IB=IG/AT
b, DG/DC=DK/KB
c, AK.BI = KI.AD
d, AK2= KG.KI








