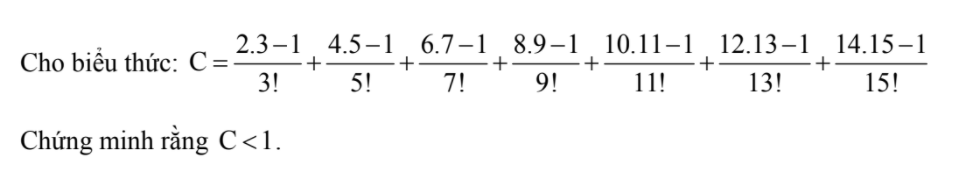\(C=\dfrac{2\cdot3-1}{1\cdot2\cdot3}+\dfrac{4\cdot5-1}{1\cdot2\cdot3\cdot4\cdot5}+...+\dfrac{14\cdot15-1}{1\cdot2\cdot...\cdot15}\\ C=1-\dfrac{1}{1\cdot2\cdot3}+\dfrac{1}{1\cdot2\cdot3}-\dfrac{1}{1\cdot2\cdot3\cdot4\cdot5}+\dfrac{1}{1\cdot2\cdot3\cdot4\cdot5}-...-\dfrac{1}{1\cdot2\cdot...\cdot13}-\dfrac{1}{1\cdot2\cdot...\cdot15}\\ C=1-\dfrac{1}{1\cdot2\cdot...\cdot15}< 1\)
Mấy anh chị ơi giúp em với
Mọi người giúp em câu B vs ah,em đang cần gấp ạ.Em cảm ơn nhiều lắm
giúp em vs ạ, em cần gấp lắm ạ :]]]
M=3/1+2 + 3/1+2+3 + 3/1+2+3+4 + ...+ 3/1+2+...+2022
so sánh M với 10/3
giúp em vs ạ, em cần gấp lắm ạ :]]]
M=3/1+2 + 3/1+2+3 + 3/1+2+3+4 + ...+ 3/1+2+...+2022
so sánh M với 10/3
ANH CHỊ ƠI GIÚP EM 2 BÀI TOÁN LỚP 7 VỚI Ạ .MAI EM KIỂM TRA GIỮA KÌ RỒI .EM CẢM ƠN RẤT NHIỀU Ạ.
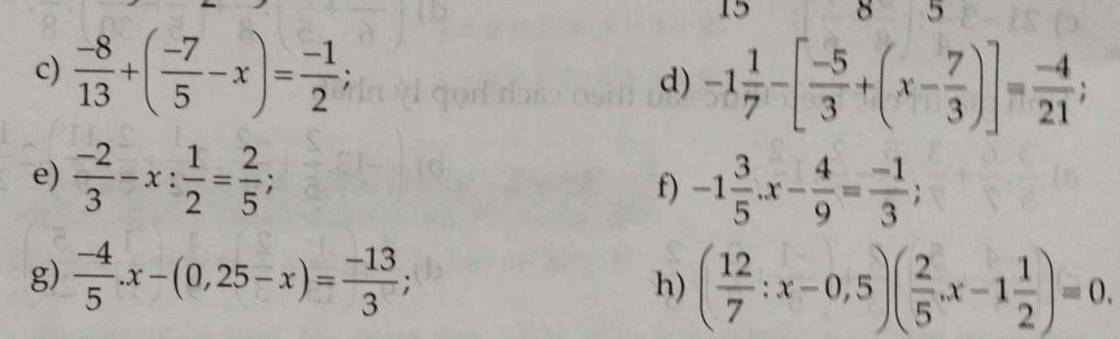Giúp em với ạ , em đang cần gấp . Em cảm ơn ạ ! =.=
Làm giúp em câu 3 với ạ , em đang cần gấp 
hi. chào các anh chị . em là HSG toán 7 nhưng có 1 số bài cô giảng em vẫn ko hiểu ạ.
giúp em với : lập bảng xét dấu là như thế nào ạ . cho ví dụ với nha
