AI GIẢI GIÚP MÌNH VỚI !!!
Bài 1. Cho tam giác ABC có o A 90 , H là trực tâm. Đường thẳng vuông góc với AB tại B cắt
đường thẳng vuông góc với AC tại C ở điểm I. Chứng minh rằng BICH là hình bình hành.
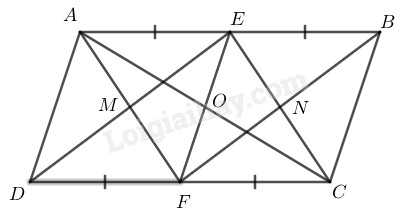
Bài 2. Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao
điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng:
a) EMFN là hình bình hành.
b) Các đường thẳng AC, EF, MN đồng quy.
Bài 3. Cho tam giác ABC có trực tâm H, kẻ Bx AB,Cy AC . Gọi D là giao điểm của Bx và
Cy.
a) Chứng minh BHCD là hình bình hành.
b) Gọi O là trung điểm của BC. Chứng minh H, O, D thẳng hàng.
Bài 4. Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho DE = BF
nhỏ hơn 1 BD
2 .
a) Chứng minh AECF là hình bình hành.
b) Gọi M, N lần lượt là giao điểm của AE, CF với DC và AB. Chứng minh AC, BD, MN đồng
quy.
Bài 5. Cho tam giác ABC cân tại A. Gọi D, E, F lần lượt là trung điểm của BC, CA và AB. Trên
tia đối của tia FC lấy H sao cho F là trung điểm của CH, các đường thẳng DE, AH cắt nhau tại I.
Chứng minh rằng các tứ giác BCAH, DCFE là hình bình hành.
Bài 2:
a) Vì \(ABCD\) là hình bình hành (gt).
=> \(AB=CD\) (tính chất hình bình hành).
=> \(AB\) // \(CD\) (định nghĩa hình bình hành).
Hay \(AE\) // \(CF.\)
+ Vì E là trung điểm của \(AB\left(gt\right)\)
=> \(AE=\frac{1}{2}AB\) (tính chất trung điểm) (1).
+ Vì F là trung điểm của \(CD\left(gt\right)\)
=> \(CF=\frac{1}{2}CD\) (tính chất trung điểm) (2).
Mà \(AB=CD\left(cmt\right)\) (3).
Từ (1), (2) và (3) => \(AE=CF.\)
Xét tứ giác \(AECF\) có:
\(AE\) // \(CF\) và \(AE=CF\left(cmt\right)\)
=> Tứ giác \(AECF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
=> \(AF\) // \(CE\) (định nghĩa hình bình hành).
Hay \(FM\) // \(EN\) (4).
+ Vì \(AB\) // \(CD\left(cmt\right)\)
=> \(BE\) // \(DF.\)
+ Vì E là trung điểm của \(AB\left(gt\right)\)
=> \(BE=\frac{1}{2}AB\) (tính chất trung điểm) (5).
+ Vì F là trung điểm của \(CD\left(gt\right)\)
=> \(DF=\frac{1}{2}CD\) (tính chất trung điểm) (6).
Từ (3), (5) và (6) => \(BE=DF.\)
Xét tứ giác \(BFDE\) có:
\(BE\) // \(DF\) và \(BE=DF\left(cmt\right)\)
=> Tứ giác \(BFDE\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
=> \(BF\) // \(DE\) (định nghĩa hình bình hành).
Hay \(FN\) // \(EM\) (7).
Từ (4) và (7) => Tứ giác \(EMFN\) là hình bình hành (định nghĩa hình bình hành).
b) Gọi O là giao điểm của \(AC\) và \(EF.\)
+ Vì \(ABCD\) là hình bình hành (gt).
=> 2 đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (tính chất hình bình hành).
=> \(AC\) đi qua trung điểm O của \(BD\) (*).
+ Vì tứ giác \(AECF\) là hình bình hành (cmt).
=> 2 đường chéo AC và EF cắt nhau tại trung điểm O của mỗi đường (tính chất hình bình hành).
=> \(EF\) đi qua trung điểm O của \(AC\) (**).
+ Vì tứ giác \(EMFN\) là hình bình hành (cmt).
=> 2 đường chéo MN và EF cắt nhau tại trung điểm O của mỗi đường (tính chất hình bình hành).
=> \(MN\) đi qua trung điểm O của \(EF\) (***).
Từ (*), (**) và (***) => \(AC,EF,MN\) đồng quy tại O (đpcm).
Chúc bạn học tốt!
mik cũng đang cần ai đó làm giúp bài 1














