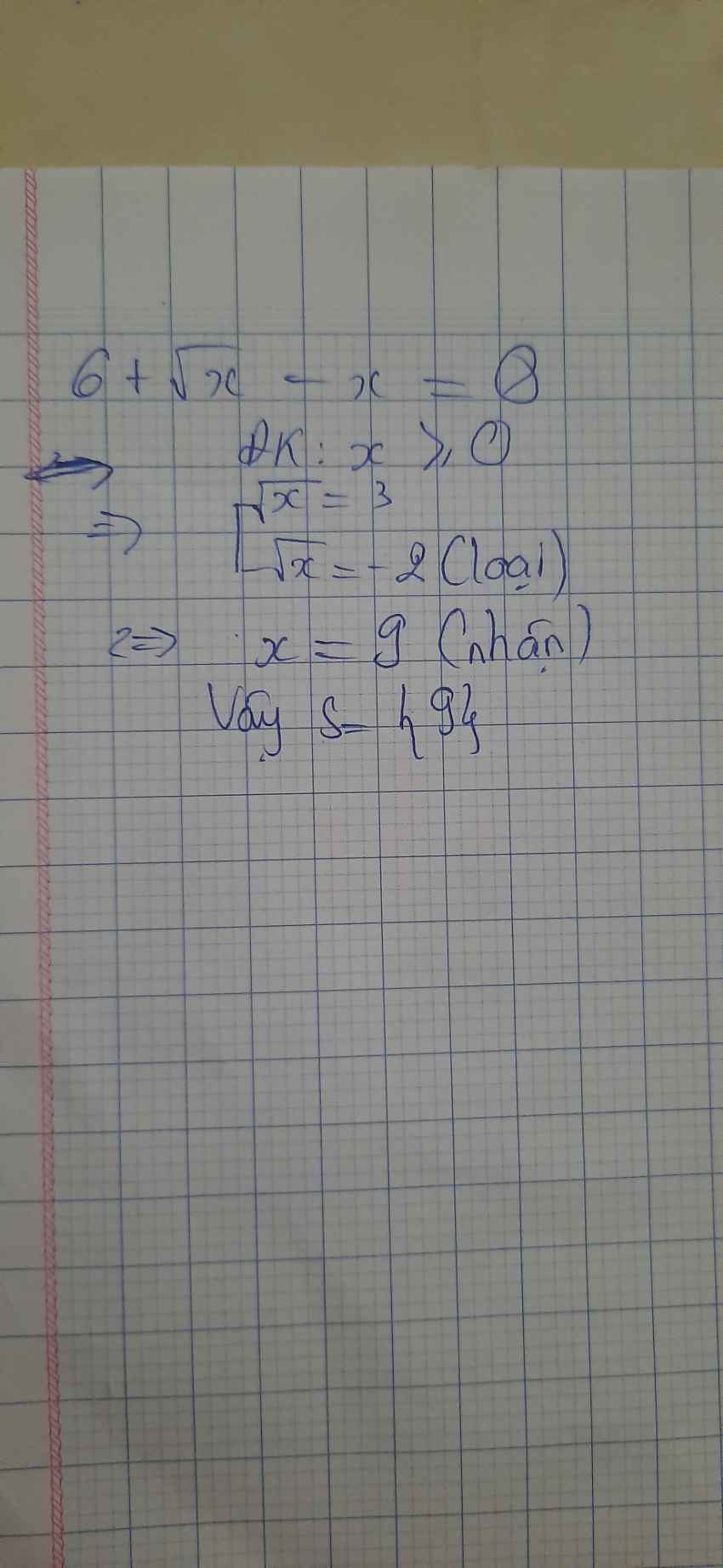ĐK: `x>=0`
`6+\sqrtx-x=0`
`6+3\sqrtx-2\sqrtx-x=0`
`<=>3(2+\sqrtx)-\sqrtx(2+\sqrtx)=0`
`<=>(\sqrtx+2)(3-\sqrtx)=0`
`<=> [(\sqrtx+2=0),(3-\sqrtx=0):}`
`<=> [(\sqrtx=-2 (L)),(\sqrtx=3):}`
`<=>x=9`
Vậy `S={9}`.
\(\rightarrow x-\sqrt{x}-6=0\)
\(\rightarrow x-3\sqrt{x}+2\sqrt{x}-6=0\)
\(\rightarrow\sqrt{x}\left(\sqrt{x}-3\right)+2\left(\sqrt{x}-3\right)=0\)
\(\rightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)=0\)
\(\rightarrow\left[{}\begin{matrix}\sqrt{x}-3=0\\\sqrt{x}+2=0\end{matrix}\right.\)
\(\rightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-2\left(voli\right)\end{matrix}\right.\)
\(\rightarrow x=9\)
Ta có: \(6+\sqrt{x}-x=0\)
\(\Leftrightarrow\left(3-\sqrt{x}\right)\left(2+\sqrt{x}\right)=0\)
\(\Leftrightarrow3-\sqrt{x}=0\)
hay x=9