Question

49. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và BAD =120^o ,SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60^o.Tính thể tích V của khối chóp S.ABCD.

Answer 1

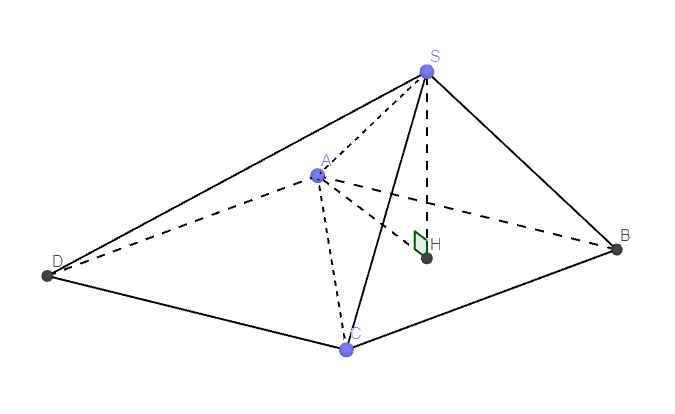
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều

Gọi H là hình chiếu vuông góc của S lên (ABC)

Do \(SA=SB=SC\Rightarrow HA=HB=HC\)

\(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp ABC

\(\Rightarrow H\) là trọng tâm tam giác ABC (do tam giác đều)

\(\Rightarrow AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)

\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và đáy

\(\Rightarrow\widehat{SAH}=60^0\)

\(\Rightarrow SH=AH.tan60^0=a\)

\(\Rightarrow V=\dfrac{1}{3}SH.2S_{ABC}=\dfrac{1}{3}a.2.\dfrac{a^2\sqrt[]{3}}{4}=\dfrac{a^3\sqrt{3}}{6}\)

Answer 2