36 phút = 0,6h
Gọi thời gian để ô tô thứ 2 tới B là t ( t>0 )
Ta có hệ phương trình :
50t = 45t + 0,6.45
<=> 5t = 27
<=> t = 5,4 h
=> AB = 5,4.50 = 270 km
Giải dùm em từ câu 5 đến câu 12 với please 😭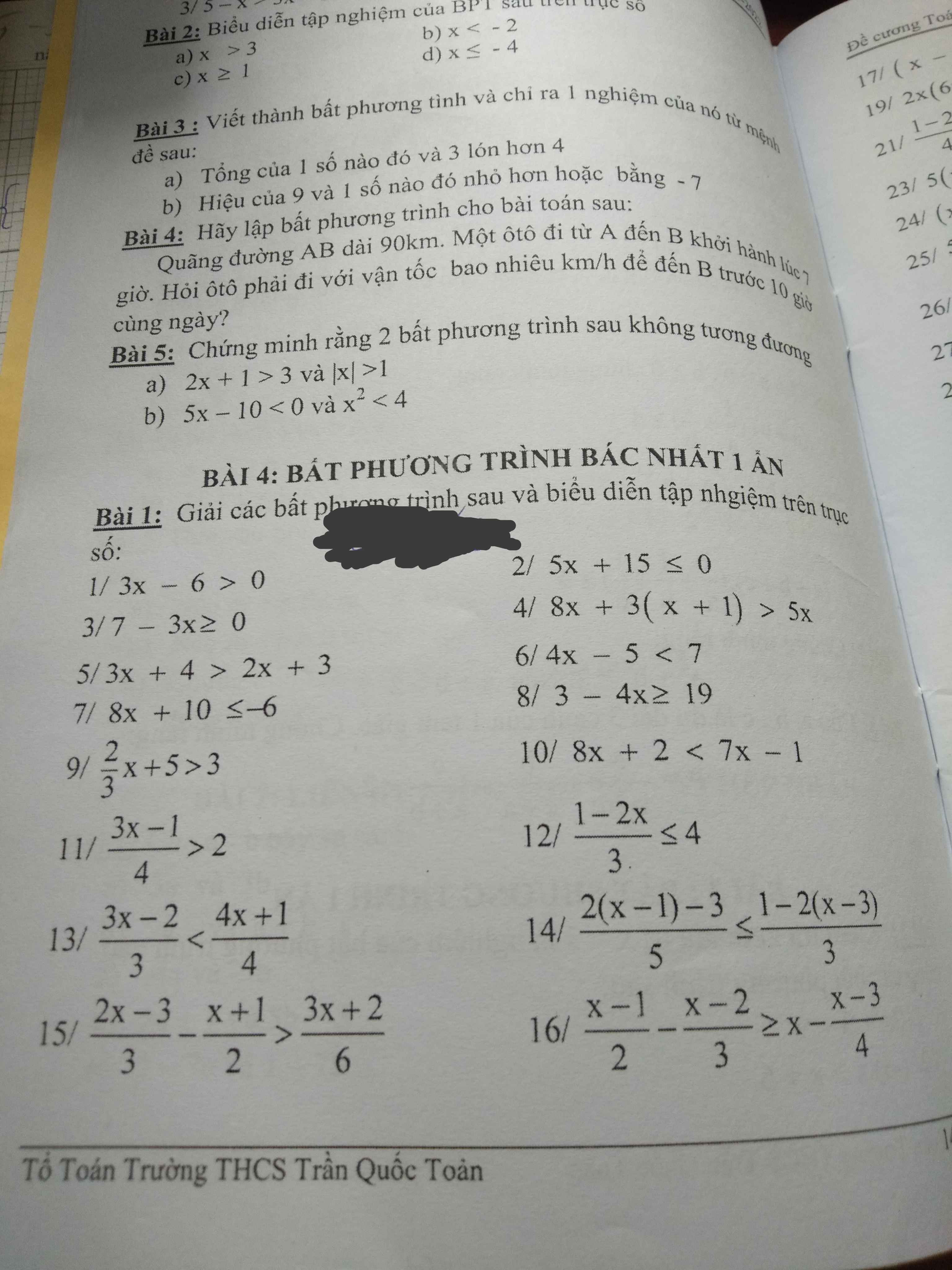
chứng minh rằng nếu a≤b thì \(\frac{-2}{3}\)a-4>\(\frac{-2}{3}\)b-4?
giúp em với ạ!!!
Với a, b, c là các số thực thỏa mãn a + b + 2c = 4. Tìm giá trị lớn nhất của các P = ab + 2bc + 4ca
Với a, b, c là các số thực dương thỏa mãn ab + bc + ca =3abc. Tìm giá trị nhỏ nhất của biểu thức P = \(\sqrt{a+b}+\sqrt{b+c}+\sqrt{a+c}\)
Chứng tỏ rằng với a và b là các số bất kì thì :
a) \(a^2+b^2-2ab\ge0\)
b) \(\dfrac{a^2+b^2}{2}\ge ab\)
Chứng minh rằng với mọi số a, b, c ta luôn có:
a. a2 + b2 \(\ge\) 2ab
b. a2 + b2 + c2 \(\ge\) ab + bc + ca
Giải phương trình sau:
a) | 2x-3 | - 4x - 9 = 0
b) (x + 1)2 - |5 - 3x| - x = x(x + 2) + 4
Em cảm ơn ạ
tìm gtln hoặc gtnn của B=2( \(\frac{x^2}{y^2}\)+\(\frac{y^2}{x^2}\))-\(\left(\frac{x}{y}+\frac{y}{x}\right)\) +1 với x,y khác 0 và xy>0 giúp mình với
1. Chứng minh rằng:
a. \(\dfrac{a^2+b^2}{2}\)≥(\(\dfrac{a+b}{2}\))2
b. \(\dfrac{a^2+b^2+c^2}{3}\)≥(\(\dfrac{a+b+c}{3}\))2
2. Chứng minh rằng:
a. a2+\(\dfrac{b^2}{4}\)≥ab
b. (a+b)2≤ 2(a2+b2)
c. a2+b2+1 ≥ ab+a+b
3. Chứng minh rằng: a2+ 5b2-(3a+b) ≥ 3ab-5
