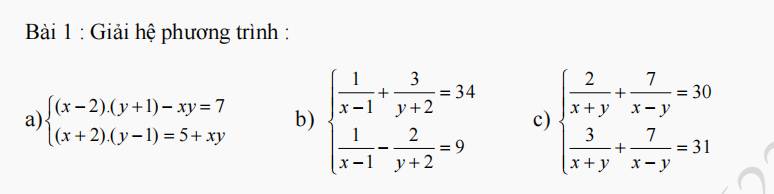a.
\(\left\{{}\begin{matrix}\left(x-2\right)\left(y+1\right)-xy=7\\\left(x+2\right)\left(y-1\right)=5+xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy+x-2y-2-xy=7\\xy-x+2y-2=5+xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=9\\-x+2y=7\end{matrix}\right.\)
Cộng vế \(\Rightarrow0=16\) (vô lý)
Vậy hệ đã cho vô nghiệm
b.
ĐKXĐ: \(x\ne1;y\ne-2\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x-1}=u\\\dfrac{1}{y+2}=v\end{matrix}\right.\) ta được:
\(\left\{{}\begin{matrix}u+3v=34\\u-2v=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5v=25\\u=2v+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v=5\\u=19\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x-1}=19\\\dfrac{1}{y+2}=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-1=\dfrac{1}{19}\\y+2=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{20}{19}\\y=-\dfrac{9}{5}\end{matrix}\right.\)
c.
ĐKXĐ: \(x\ne\pm y\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+y}=u\\\dfrac{1}{x-y}=v\end{matrix}\right.\) ta được:
\(\left\{{}\begin{matrix}2u+7v=30\\3u+7v=31\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=\dfrac{30-2u}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}=1\\\dfrac{1}{x-y}=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+y=1\\x-y=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{8}\\y=\dfrac{3}{8}\end{matrix}\right.\)