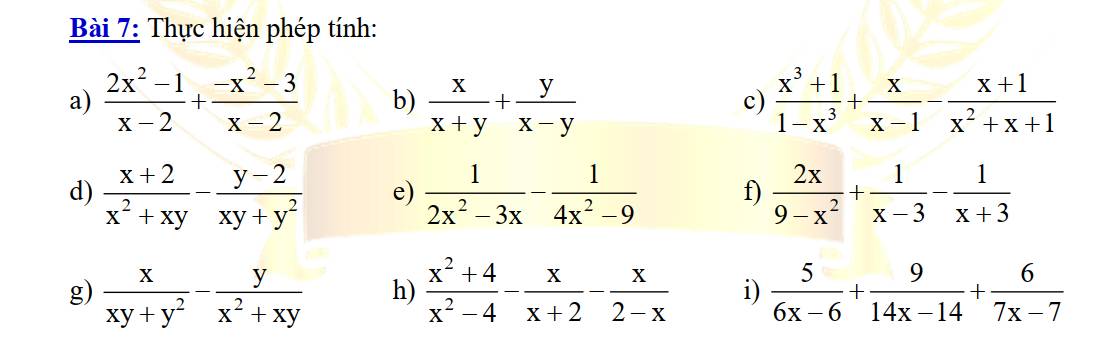a: ĐKXĐ: x<>2
\(\dfrac{2x^2-1}{x-2}+\dfrac{-x^2-3}{x-2}\)
\(=\dfrac{2x^2-1-x^2-3}{x-2}\)
\(=\dfrac{x^2-4}{x-2}=\dfrac{\left(x-2\right)\left(x+2\right)}{x-2}=x+2\)
b: ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{x}{x+y}+\dfrac{y}{x-y}\)
\(=\dfrac{x\left(x-y\right)+y\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2-xy+xy+y^2}{x^2-y^2}=\dfrac{x^2+y^2}{x^2-y^2}\)
c: ĐKXĐ: x<>1
\(\dfrac{x^3+1}{1-x^3}+\dfrac{x}{x-1}-\dfrac{x+1}{x^2+x+1}\)
\(=\dfrac{-x^3-1}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x}{x-1}-\dfrac{x+1}{x^2+x+1}\)
\(=\dfrac{-x^3-1+x\left(x^2+x+1\right)-\left(x+1\right)\cdot\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-x^3-1+x^3+x^2+x-x^2+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x}{x^3-1}\)
d: ĐKXĐ: x<>0; y<>0; x<>-y
\(\dfrac{x+2}{x^2+xy}-\dfrac{y-2}{xy+y^2}\)
\(=\dfrac{x+2}{x\left(x+y\right)}-\dfrac{y-2}{y\left(x+y\right)}\)
\(=\dfrac{y\left(x+2\right)-x\left(y-2\right)}{xy\left(x+y\right)}\)
\(=\dfrac{xy+2y-xy+2x}{xy\left(x+y\right)}=\dfrac{2\left(x+y\right)}{xy\left(x+y\right)}=\dfrac{2}{xy}\)
e: ĐKXĐ: \(x\notin\left\{0;\dfrac{3}{2};-\dfrac{3}{2}\right\}\)
\(\dfrac{1}{2x^2-3x}-\dfrac{1}{4x^2-9}\)
\(=\dfrac{1}{x\left(2x-3\right)}-\dfrac{1}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{2x+3-x}{x\left(2x-3\right)\left(2x+3\right)}=\dfrac{x+3}{x\left(2x-3\right)\left(2x+3\right)}\)
f: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\dfrac{2x}{9-x^2}+\dfrac{1}{x-3}-\dfrac{1}{x+3}\)
\(=\dfrac{-2x}{\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x-3}-\dfrac{1}{x+3}\)
\(=\dfrac{-2x+x+3-x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2x+6}{\left(x-3\right)\left(x+3\right)}=-\dfrac{2}{x+3}\)
g:
ĐKXĐ: x<>0; y<>0; x<>-y
\(\dfrac{x}{xy+y^2}-\dfrac{y}{x^2+xy}\)
\(=\dfrac{x}{y\left(x+y\right)}-\dfrac{y}{x\left(x+y\right)}\)
\(=\dfrac{x^2-y^2}{xy\left(x+y\right)}=\dfrac{\left(x-y\right)\left(x+y\right)}{xy\left(x+y\right)}=\dfrac{x-y}{xy}\)
h: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x^2+4}{x^2-4}-\dfrac{x}{x+2}-\dfrac{x}{2-x}\)
\(=\dfrac{x^2+4}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x+2}+\dfrac{x}{x-2}\)
\(=\dfrac{x^2+4-x\left(x-2\right)+x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4-x^2+2x+x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
i: ĐKXĐ: x<>1
\(\dfrac{5}{6x-6}+\dfrac{9}{14x-14}+\dfrac{6}{7x-7}\)
\(=\dfrac{5}{6\left(x-1\right)}+\dfrac{9}{14\left(x-1\right)}+\dfrac{6}{7\left(x-1\right)}\)
\(=\dfrac{1}{x-1}\left(\dfrac{5}{6}+\dfrac{9}{14}+\dfrac{6}{7}\right)\)
\(=\dfrac{1}{x-1}\cdot\left(\dfrac{35}{42}+\dfrac{27}{42}+\dfrac{36}{42}\right)\)
\(=\dfrac{1}{x-1}\cdot\dfrac{98}{42}=\dfrac{7}{3\left(x-1\right)}\)