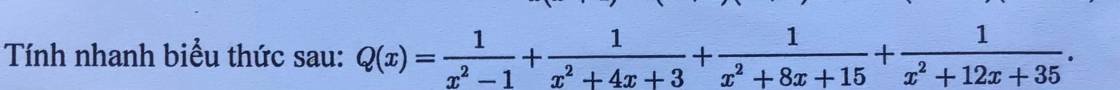\(Q\left(x\right)=\dfrac{1}{x^2-1}+\dfrac{1}{x^2+4x+3}+\dfrac{1}{x^2+8x+15}+\dfrac{1}{x^2+12x+35}\)
\(=\dfrac{1}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x^2+x+3x+3}+\dfrac{1}{x^2+3x+5x+15}+\dfrac{1}{x^2+5x+7x+35}\)
\(=\dfrac{1}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x\left(x+1\right)+3\left(x+1\right)}+\dfrac{1}{x\left(x+3\right)+5\left(x+3\right)}+\dfrac{1}{x\left(x+5\right)+7\left(x+5\right)}\)
\(=\dfrac{1}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+7\right)}\)
\(=\dfrac{1}{2}\cdot\left[\dfrac{2}{\left(x-1\right)\left(x+1\right)}+\dfrac{2}{\left(x+1\right)\left(x+3\right)}+\dfrac{2}{\left(x+3\right)\left(x+5\right)}+\dfrac{2}{\left(x+5\right)\left(x+7\right)}\right]\)
\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+7}\right)\)
\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{x-1}-\dfrac{1}{x+7}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{x+7-\left(x-1\right)}{\left(x-1\right)\left(x+7\right)}\)
\(=\dfrac{1}{2}\cdot\dfrac{8}{\left(x-1\right)\left(x+7\right)}\)
\(=\dfrac{4}{\left(x-1\right)\left(x+7\right)}\)
\(=\dfrac{4}{x^2+6x-7}\)
#\(Toru\)