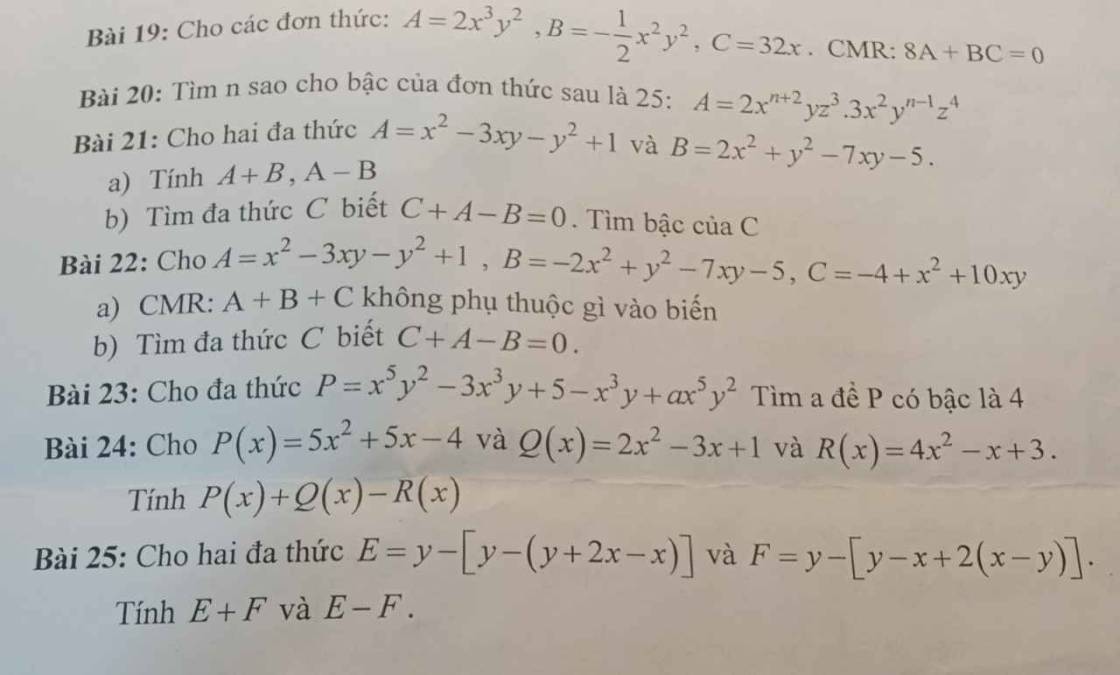Bài 23:
\(P=x^5y^2-3x^3y+5-x^3y+ax^5y^2=\left(1+a\right)x^5y^2-4x^3y+5\\ Ta.có:x^5y^2\Rightarrow bậc.7\\ -4x^3y\Rightarrow Bậc.4\\ 5:Bậc.0\\ Vậy:P.đa.thức.bậc.4\Leftrightarrow1+a=0\Leftrightarrow a=-1\\ Vậy:a=-1\)
\(Bài.22:A=x^2-3xy-y^2+1;B=-2x^2+y^2-7xy-5;C=-4+x^2+10xy\\ a,A+B+C=\left(x^2-3xy-y^2+1\right)+\left(-2x^2+y^2-7xy-5\right)+\left(-4+x^2+10xy\right)\\ =\left(x^2-2x^2+x^2\right)+\left(y^2-y^2\right)-\left(7xy+3xy-10xy\right)+1-5-4=-8\)
Vậy: A+B+C không phụ thuộc gì vào biến
\(b,C+A-B=0\\ \Leftrightarrow C=B-A=\left(-2x^2+y^2-7xy-5\right)-\left(x^2-3xy-y^2+1\right)\\ =\left(-2x^2-x^2\right)+\left(y^2+y^2\right)-\left(7xy-3xy\right)-\left(5+1\right)\\ =-3x^2+2y^2-4xy-6\)
Bài 20:
Bậc của đơn thức là 25
<=> (n+2)+1+3+2 + (n-1)+4=25
<=> 2n+11=25
<=>2n=25-11
<=>2n=14
<=>n=14:2=7
Vậy n=7