Đặt \(A=3+3^2+3^3+...+3^{1012}\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{1013}\)
\(\Rightarrow3A-A=\left(3^2+3^3+3^4+...+3^{1013}\right)-\left(3+3^2+3^3+...+3^{1012}\right)\)
\(\Rightarrow2A=3^{1013}-3\)
\(\Rightarrow A=\dfrac{3^{1013}-3}{2}\)
\(\Rightarrow B=\dfrac{A}{3^{1013}-3}=\dfrac{\dfrac{3^{1013}-3}{2}}{3^{1013}-3}\)
\(\Rightarrow B=\dfrac{1}{2}\)
Đặt A = 3 + 3² + 3³ + ... + 3¹⁰¹²
⇒ 3A = 3² + 3³ + 3⁴ + ... + 3¹⁰¹³
⇒ 2A = 3A - A
= (3² + 3³ + 3⁴ + ... + 3¹⁰¹³) - (3 + 3² + 3³ + ... + 3¹⁰¹²)
= 3¹⁰¹³ - 3
⇒ A = (3¹⁰¹³ - 3)/2
⇒ B = A/(3¹⁰¹³ - 3)
= (3¹⁰¹³ - 3)/[2(3¹⁰¹³ - 3)]
= 1/2

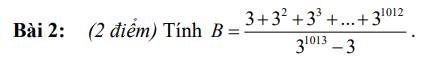














 mk cảm ơn ạ
mk cảm ơn ạ 
