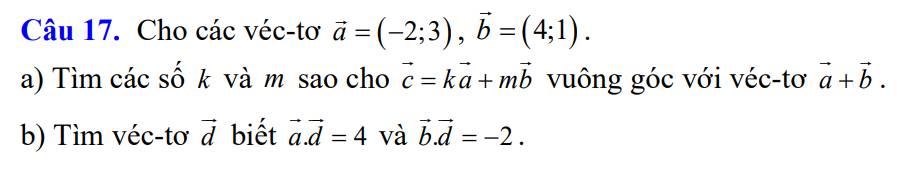a: \(c=\overrightarrow{a}\cdot k+\overrightarrow{b}\cdot m\)
=>\(c=\left(-2k+4m;3k+m\right)\)
\(\overrightarrow{c}\perp\overrightarrow{a}+\overrightarrow{b}\)
\(\overrightarrow{c}=\left(-2k+4m;3k+m\right);\overrightarrow{a}+\overrightarrow{b}=\left(2;4\right)\)
Do đó: \(2\left(-2k+4m\right)+4\left(3k+m\right)=0\)
=>\(-4k+8m+12k+4m=0\)
=>8k+12m=0
=>2k+3m=0
=>\(k=-\dfrac{3m}{2}\)
b: Gọi tọa độ của vecto d là (x,y)
\(\overrightarrow{a}\cdot\overrightarrow{d}=4\)
=>\(-2x+3y=4\)(1)
\(\overrightarrow{b}\cdot\overrightarrow{d}=-2\)
=>\(4x+y=-2\)(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2x+3y=4\\4x+y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+6y=8\\4x+y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=6\\4x+y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{6}{7}\\4x=-2-y=-\dfrac{20}{7}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{5}{7}\\y=\dfrac{6}{7}\end{matrix}\right.\)