Bài 17 :
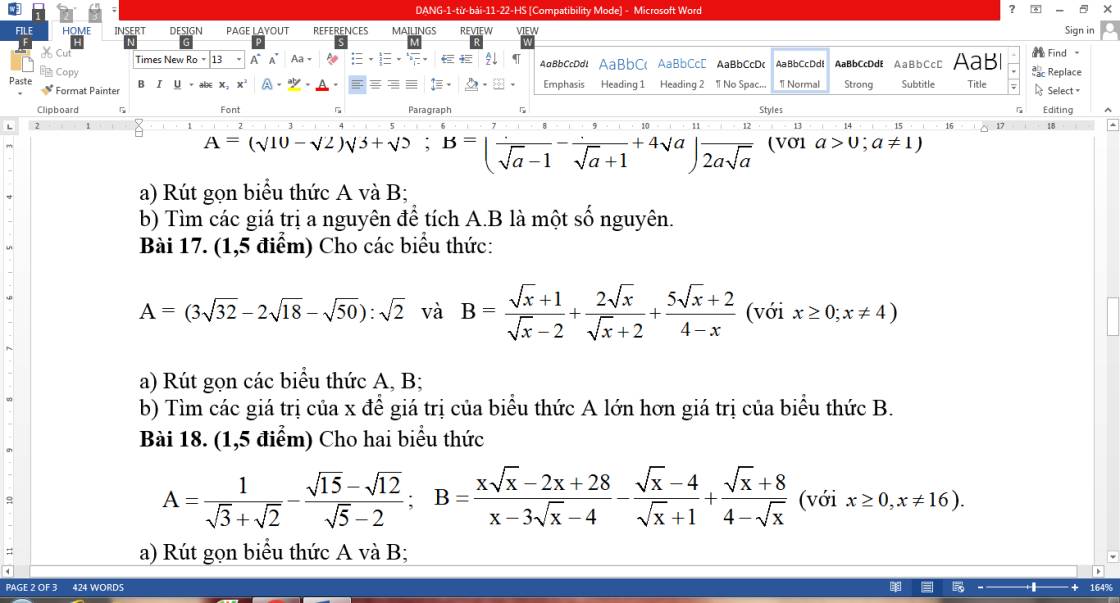
\(a,\) \(A=\left(3\sqrt{32}-2\sqrt{18}-\sqrt{50}\right):\sqrt{2}\)
\(=\left(3.4\sqrt{2}-2.3\sqrt{2}-5\sqrt{2}\right):\sqrt{2}\)
\(=\left(12\sqrt{2}-6\sqrt{2}-5\sqrt{2}\right):\sqrt{2}\)
\(=\sqrt{2}.\dfrac{1}{\sqrt{2}}\)
\(=1\)
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\left(dkxd:x\ge0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+2\sqrt{x}\left(\sqrt{x}-2\right)-\left(5\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
\(b,\) Để \(A>B\Leftrightarrow1>\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
\(\Leftrightarrow\dfrac{3\sqrt{x}-\sqrt{x}-2}{\sqrt{x}+2}< 0\)
\(\Leftrightarrow2\sqrt{x}-2< 0\)
\(\Leftrightarrow2\sqrt{x}< 2\)
\(\Leftrightarrow\sqrt{x}< 1\)
\(\Leftrightarrow x< 1\)