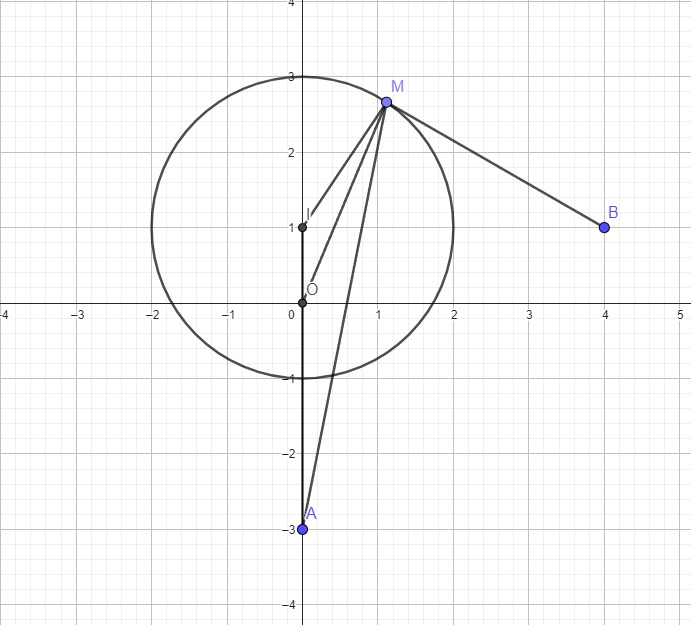
Chà bài toán khó chịu thật, phải vẽ hẳn hình ra mới thấy được hướng giải:
Đường tròn (C) tâm \(I\left(0;1\right)\) bán kính \(R=2\)
\(\overrightarrow{IO}=\left(0;-1\right)\Rightarrow IO=1\)
\(\overrightarrow{IA}=\left(0;-4\right)\Rightarrow IA=4=2R=2IM\)
Xét hai tam giác MIO và AIM có:
\(\left\{{}\begin{matrix}\dfrac{IM}{IA}=\dfrac{IO}{IM}=\dfrac{1}{2}\\\widehat{MIO}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta MIO\sim\Delta AIM\left(c.g.c\right)\)
\(\Rightarrow\dfrac{OM}{AM}=\dfrac{IO}{IM}=\dfrac{1}{2}\Rightarrow AM=2OM\)
\(\Rightarrow P=2\left(OM+MB\right)\ge2OB\)
Dấu "=" xảy ra khi và chỉ khi M là giao điểm OB và (C)
\(P_{min}=2OB=2\sqrt{17}\)