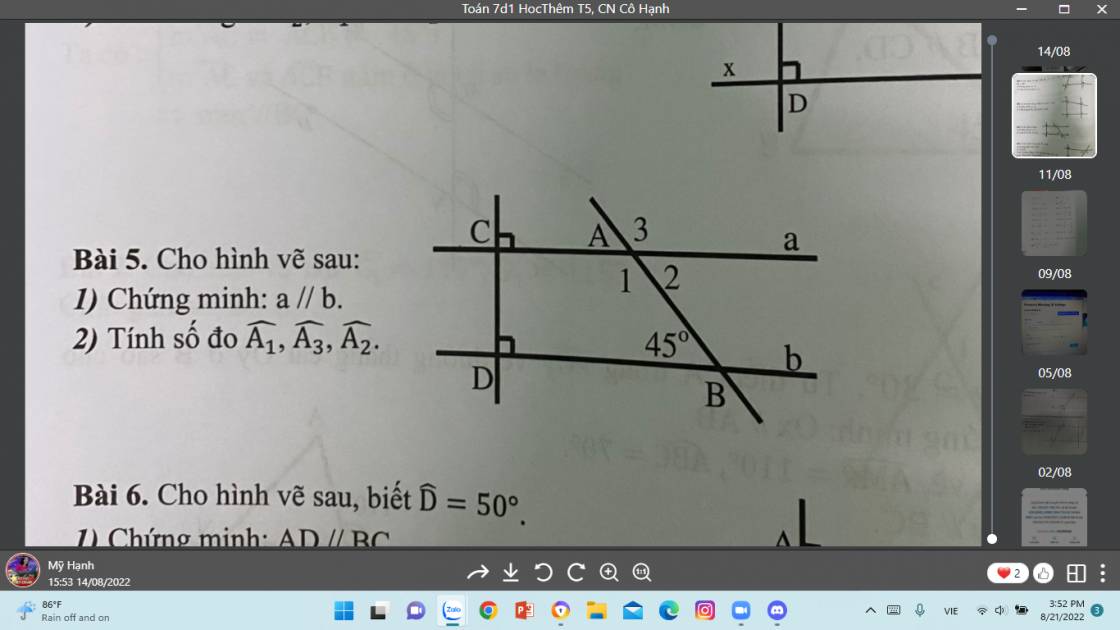
1) Theo đề bài ta có `{(CD bot a),(CD bot b):}`
`=> a //b ` ( từ vuông góc đến song song)
2) Ta có `a//b`
`=> hat{DBA} = hat{A_2}` ( hai góc so le trong)
`=> hat{DBA} = hat{A_2} =45^o`
Lại có : ` hat{A_1} + hat{A_2} =180^0` ( kề bù)`
`=> hat{A_1} = 180^0 - hat{A_2} = 180^0 -45^0 = 135^0`
mà `hat{A_1} =hat{A_3} ` ( đối đỉnh)
`=> hat{A_1} =hat{A_3} = 135^0`
Vậy `hat{A_1} =135^0`
`hat{A_3} =135^0`
`hat{A_2} = 45^0`
1, \(\left[{}\begin{matrix}CD\perp a\\CD\perp b\end{matrix}\right.\Rightarrow a//b\)
2, góc \(A_2=B_1=45\) (hai góc sole trong)
góc \(A_1=180-A_2=180-45=135độ\) (hai góc kề bù)
góc \(A_3=A_1=135độ\) (hai góc đối đỉnh)