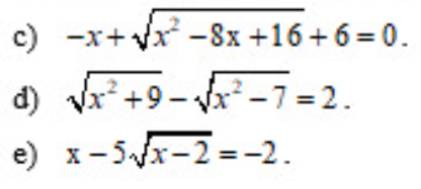`c, -x + x - 4 + 6 = 0`
`=> 2 = 0`
`->` Vô lý.
c) \(-x+\sqrt{x^2-8x+16}+6=0\)
\(\Leftrightarrow\sqrt{\left(x-4\right)^2}=x-6\)
\(\Leftrightarrow\left|x-4\right|=x-6\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-6\ge0\\\left[{}\begin{matrix}x-4=x-6\\x-4=6-x\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge6\\\left[{}\begin{matrix}0x=-2\left(PTVN\right)\\x=5\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow x\in\varnothing\)
- Vậy \(S=\varnothing\)
d) \(\sqrt{x^2+9}-\sqrt{x^2-7}=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-7\ge0\\\sqrt{x^2+9}=\sqrt{x^2-7}+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\ge0\\x^2+9=x^2-7+4\sqrt{x^2-7}+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\sqrt{7}\\x\le-\sqrt{7}\end{matrix}\right.\\4\sqrt{x^2-7}=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\sqrt{7}\\x\le-\sqrt{7}\end{matrix}\right.\\\sqrt{x^2-7}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\sqrt{7}\\x\le-\sqrt{7}\end{matrix}\right.\\x^2-7=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\sqrt{7}\\x\le-\sqrt{7}\end{matrix}\right.\\\left(x-4\right)\left(x+4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\sqrt{7}\\x\le-\sqrt{7}\end{matrix}\right.\\\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
- Vậy \(S=\left\{4;-4\right\}\)
e) \(x-5\sqrt{x-2}=-2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2\ge0\\\left(x-2\right)-5\sqrt{x-2}+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\\left(x-2\right)-\sqrt{x-2}-4\sqrt{x-2}+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2\ge0\\\sqrt{x-2}\left(\sqrt{x-2}-1\right)-4\left(\sqrt{x-2}-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\\left(\sqrt{x-2}-1\right)\left(\sqrt{x-2}-4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2\ge0\\\left[{}\begin{matrix}\sqrt{x-2}-1=0\\\sqrt{x-2}-4=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\\left[{}\begin{matrix}x=3\left(nhận\right)\\x=18\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=18\end{matrix}\right.\)
- Vậy \(S=\left\{3;18\right\}\)