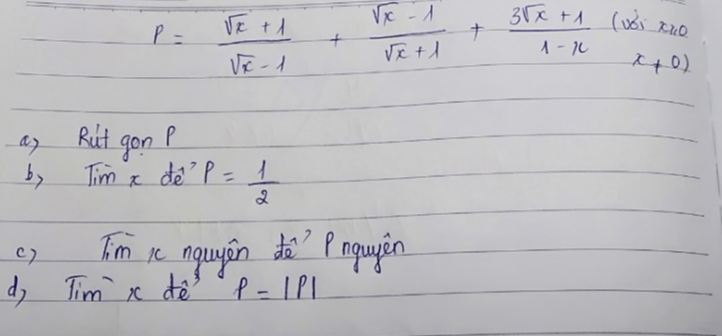`a, (sqrt x + 1)/(sqrt x - 1) + (sqrt x - 1)/(sqrt x + 1) + ( 3 sqrt x + 1)/(1-x)`
`= (sqrt x+1)^2/(x-1) + (sqrt x - 1)^2/(x-1) - (3 sqrt x +1)/(x-1)`
`= (x + 2 sqrt x + 1 + x - 2 sqrt x + 1 - 3 sqrt x - 1)/(x-1)`
`= (2x - 3 sqrt x + 1)/(x-1)`
`= (2 sqrt x-1)/(sqrt x +1)`
`b, P = 1/2 => (2 sqrt x - 1)/(sqrt x +1 ) = 1/2`
`=> 4 sqrt x - 2 = sqrt x + 1`
`<=> 3 sqrt x = 3`
`=> sqrt x = 1 => x = 1`.
`c, P in ZZ => (2sqrtx-1)/(sqrtx+1) in ZZ`
`=> 2 sqrt x - 1 vdots sqrt x +1`
`=> 2 sqrt x + 2 - 3 vdots sqrt x + 1`
`=> -3 vdots sqrt x + 1`
`=> sqrt x +1 in Ư(3)`
`=> sqrt x + 1 in {+-1, +-3}`
`=> x = 0, 4`.
`d, P = |P| => P >=0`
`=> (2sqrtx-1)/(sqrtx+1) >=0`.
`Th1: {(2 sqrt x - 1 >=0), (sqrt x + 1 >0):}`
`=> {(x >= 1/4), (x > -1):}`
`=> x >= 1/4`.
`Th2: {(2 sqrt x - 1 <=0), (sqrt x + 1 < 0):}`
`=> {(x <= 1/4), (x < -1):}`
`=> x <= -1`.
Vậy `1/4 <= x <= -1` thì `P = |P|`
a.
\(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(P=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(P=\dfrac{\left(\sqrt{x}+1\right)^2}{x-1}+\dfrac{\left(\sqrt{x}-1\right)^2}{x-1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(P=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{x-1}\)
\(P=\dfrac{2x-3\sqrt{x}+1}{x-1}=\dfrac{2x-2\sqrt{x}-\sqrt{x}+1}{x-1}\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{x-1}\)
\(P=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
b.
<=> \(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{1}{2}\)
<=> \(2\left(2\sqrt{x}-1\right)=\sqrt{x}+1\)
<=> \(4\sqrt{x}-2-\sqrt{x}-1=0\)
<=> \(3\sqrt{x}-3=0\)
<=> \(3\sqrt{x}=3\)
<=> \(\sqrt{x}=1\)
=> x = 1