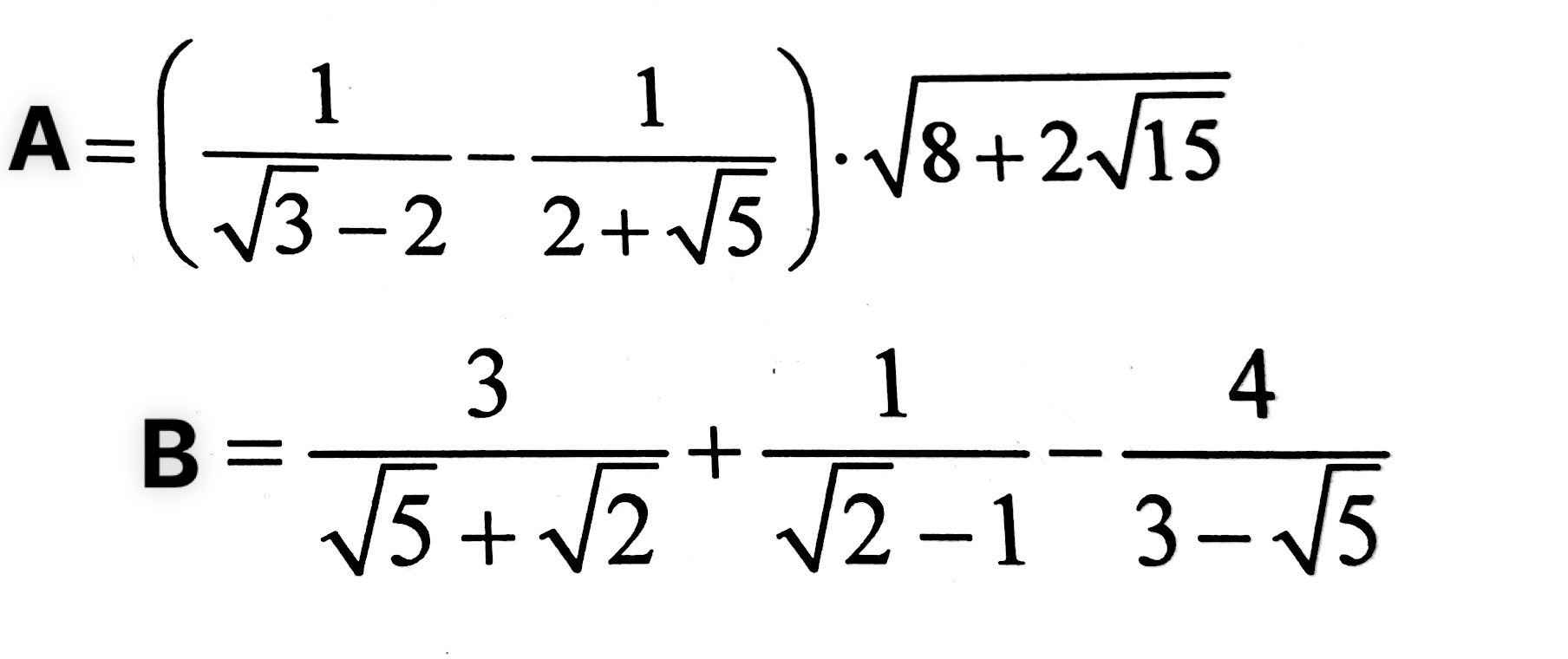a: \(A=\left(\dfrac{-1}{2-\sqrt{3}}-\dfrac{1}{\sqrt{5}+2}\right)\cdot\left(\sqrt{5}+\sqrt{3}\right)\)
\(=\left(-2-\sqrt{3}-\sqrt{5}+2\right)\cdot\left(\sqrt{5}+\sqrt{3}\right)\)
\(=-8-2\sqrt{15}\)
b: \(B=\sqrt{5}-\sqrt{2}+\sqrt{2}+1-3-\sqrt{5}=-2\)
`A=(1/[\sqrt{3}-2]-1/[2+\sqrt{5}]).\sqrt{8+2\sqrt{15}}`
`A=([\sqrt{3}+2]/[3-4]-[2-\sqrt{5}]/[4-5]).\sqrt{3+2\sqrt{3}.\sqrt{5}+5}`
`A=(-\sqrt{3}-2+2-\sqrt{5})\sqrt{(\sqrt{3}+\sqrt{5})^2}`
`A=(-\sqrt{3}-\sqrt{5}).|\sqrt{3}+\sqrt{5}|`
`A=-(\sqrt{3}+\sqrt{5})(\sqrt{3}+\sqrt{5})`
`A=-(\sqrt{3}+\sqrt{5})^2=-(3+5+2\sqrt{15})=-8-2\sqrt{5}`
_______________________________________________________
`B=3/[\sqrt{5}+\sqrt{2}]+1/[\sqrt{2}-1]-4/[3-\sqrt{5}]`
`B=[3(\sqrt{5}-\sqrt{2})]/[5-2]+[\sqrt{2}+1]/[2-1]-[4(3+\sqrt{5})]/[9-5]`
`B=\sqrt{5}-\sqrt{2}+\sqrt{2}+1-3-\sqrt{5}`
`B=-2`