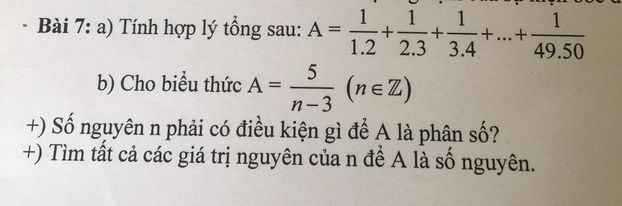a, \(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{59}-\dfrac{1}{50}=1-\dfrac{1}{50}=\dfrac{49}{50}\)
b, đk : n khác 3
\(\Rightarrow n-3\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
| n-3 | 1 | -1 | 5 | -5 |
| n | 4 | 2 | 8 | -2 |
a) \(=>A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(A=1-\dfrac{1}{50}=\dfrac{50}{50}-\dfrac{1}{50}=\dfrac{49}{50}\)
b) để A∈Z
\(=>n-3\inƯ\left(5\right)=\left\{-1,1,-5,5\right\}\)
\(=>\left\{{}\begin{matrix}n-3=1\\n-3=-1\\n-3=5\\n-3=-5\end{matrix}\right.=>\left\{{}\begin{matrix}n=4\\n=2\\n=8\\n=-2\end{matrix}\right.\)