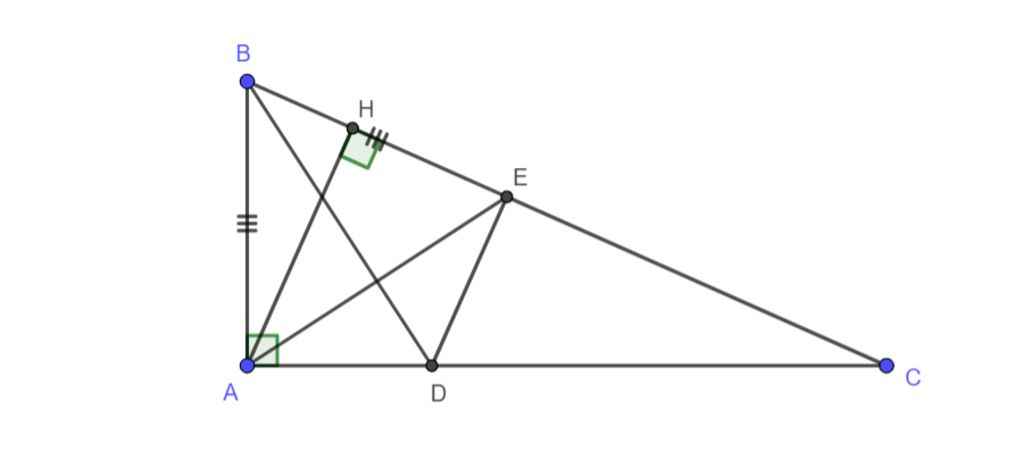
![]()
a) Xét tam giác ABD và tam giác EBD có:
AB=BE (giả thiết)
ˆABD=ˆABDABD^=ABD^ (BD là tia phân giác của góc B)
BD chung
⇒⇒ tam giác ABD = tam giác EBD (c-g-c) (1)
⇒⇒ ˆA=ˆBED=90oA^=BED^=90o
⇒⇒ DE vuông góc BE
b) Do BA=BE⇒B∈BA=BE⇒B∈ đường trung trực của AE (2)
Ta lại có DA=DEDA=DE (hai cạnh tương ứng bằng nhau suy ra từ (1))
⇒D∈⇒D∈ đường trung trực của AE (3)
Từ (2) và (3) suy ra đường trung trực của AE đi qua 2 điểm B và D
hay BDBD là đường trung trực của AE
c) Trong tam giác AHE vuông tại H có góc AEH nhọn
⇒⇒ ˆAECAEC^ là góc tù
⇒⇒ ΔAECΔAEC có ˆACE<ˆAECACE^<AEC^
⇒⇒ AE < AC (quan hệ giữa cạnh và góc đối diện)
mà EH là hình chiếu của AE trên BC.
và HC là hình chiếu của AC trên BC.
⇒⇒ EH < HC (quan hệ đường xiên và hình chiếu).












