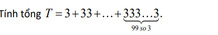\(T=\dfrac{1}{3}.9+\dfrac{1}{3}.99+...+\dfrac{1}{3}.999...9\)
\(=\dfrac{1}{3}\left(10^1-1\right)+\dfrac{1}{3}\left(10^2-1\right)+...+\dfrac{1}{3}\left(10^{99}-1\right)\)
\(=\dfrac{1}{3}\left(10^1+10^2+...+10^{99}\right)-\dfrac{1}{3}.99\)
\(=\dfrac{1}{3}.10.\dfrac{10^{99}-1}{10-1}-33=\dfrac{10^{100}-10}{27}-33\)
Tìm u1 và công bội q của cấp số nhân (un) biết :
a/ \(\left\{{}\begin{matrix}u_4-u_2=72\\u_5-u_3=144\end{matrix}\right.\)
b/ \(\left\{{}\begin{matrix}u_1-u_3+u_5=65\\u_1+u_7=325\end{matrix}\right.\)
c/ \(\left\{{}\begin{matrix}u_1+u_3+u_5=-21\\u_2+u_4=10\end{matrix}\right.\)
Cho năm số a , b , c , d , e tạo thành một cấp số nhân theo thứ tự đó và các số đều khác 0 , biết \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}+\frac{1}{e}=10\) và tổng của chúng bằng 40 . Tính giá trị \(\left|S\right|\) với S = abcde
A. \(\left|S\right|=42\)
B. \(\left|S\right|=62\)
C. \(\left|S\right|=32\)
D. \(\left|S\right|=52\)
Nếu \(lim\) (x->1) \(\dfrac{f\left(x\right)-5}{x-1}=2\) và lim (x->1) \(\dfrac{g\left(x\right)-1}{x-1}=3\) thì lim (x->1) \(\dfrac{\sqrt{f\left(x\right).g\left(x\right)+4}-3}{x-1}\) bằng mấy
Tìm số các số hạng của cấp số nhân \(\left(u_n\right)\) biết :
a) \(q=2\) \(u_n=96\) \(S_n=189\)
b) \(u_1=2\) \(u_n=\dfrac{1}{8}\) \(S_n=\dfrac{31}{8}\)
Ba số khác nhau có tổng bằng 114 có thể coi là ba số hạng liên tiếp của một cấp số nhân, hoặc coi là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng. Tìm các số đó ?
Cho 3 số : x; 3; y lập thành một cấp số nhân và \(x^4=y\sqrt{3}\). Tìm x, y và công bội q của cấp số đó ?
Chứng minh rằng : Nếu \(0 > N\)\(\ne1\) điều kiện ắt có và đủ để ba số dương a, b, c tạo thành một cấp số nhân (theo thứ tự đó) là :
\(\frac{\log_aN}{\log_cN}=\frac{\log_aN-\log_bN}{\log_bN-\log_cN}\) \(\left(a,b,c\ne1\right)\)
Giải chi tiết bài này giúp em với ạ
giúp em với ạ
