Câu 13
Áp dụng định lsi Pytago : \(AB^2+BC^2=AC^2\)
\(=>BC=\sqrt{AC^2-AB^2}=\sqrt{9^2-6^2}=3\sqrt{5}\) cm
Câu 14 Tự vẽ hình
Xét tam giác BEM và tam giác CFM
góc E = góc F = 90 độ ( BE, CF vuông góc vs Ax-gt)
góc EMB = góc FMC ( đối đỉnh)
BM = MC ( M là trung điểm BC -gt)
=>tam giác BEM = tam giác CFM ( cạnh huyền góc nhọn )
=> BE = CF
Câu 15
Tự vẽ hình ='))
Xét tam giác AEC và tam giác ADB cs
AC = AB ( Tam giác ABC cân tại A -gt)
góc A chung
AE = AD ( gt)
=> tam giác AEC = tam giác ADB ( c-g-c)
=> gsoc ABD = góc ACE
Câu 13 :
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AC^2-AB^2}=3\sqrt{5}cm\)
Câu 14 : Xét tam giác BEM và tam giác FCM có :
^EMB = ^CMF (đối đỉnh)
^BEM = ^FCM = 900
BM = MC (gt)
Vậy tam giác BEM = tam giác FCM (ch-gn)
=> BE = FC (2 cạnh tương ứng)
Câu 13:
Xét \(\Delta ABC\left(\widehat{B}=90^o\right)\) có:
\(AC^2=AB^2+BC^2\) (định lí pitago)
\(\Rightarrow BC=\sqrt{AC^2-AB^2}=\sqrt{9^2-6^2}=3\sqrt{5}\left(cm\right)\)
Vậy: \(BC=3\sqrt{5}cm\)
Câu 14:
Xét \(\Delta BEM\left(\widehat{E}=90^o\right)\) và \(\Delta CFM\left(\widehat{F}=90^o\right)\) có:
\(BM=CM\) (giả thiết)
\(\widehat{BME}=\widehat{CMF}\) (\(2\) góc đối đỉnh)
\(\Rightarrow\Delta BEM=\Delta CFM\left(ch.gn\right)\)
\(\Rightarrow BE=CF\) (\(2\) cạnh tương ứng)
Câu 15:
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{A}\) chung
\(AD=AE\) (giả thiết)
\(\Rightarrow\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\) (\(2\) góc tương ứng)
Câu 13 :
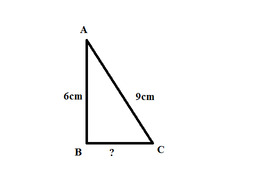
Áp dụng định lý Pytago ta có :
\(BC^2=AC^2-AB^2\)
-> \(BC^2=45\)
-> \(BC=\sqrt{45}\left(cm\right)\)




















