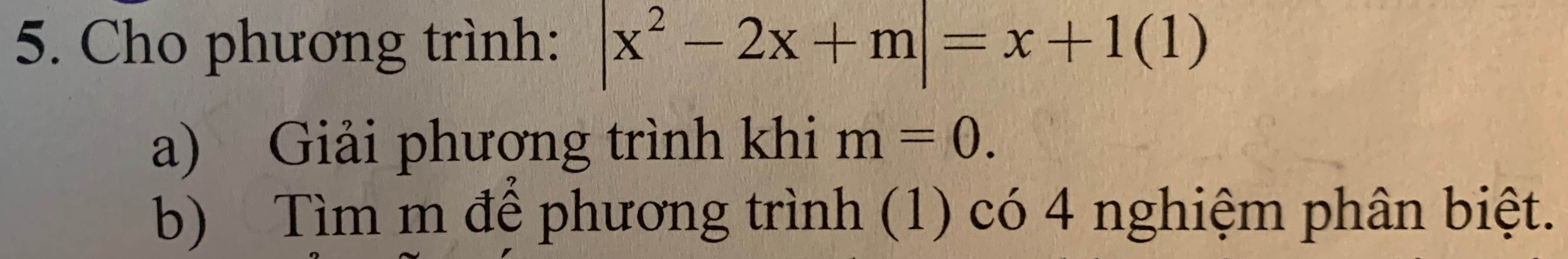18.
Hình vẽ:
\(AH^2=\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cosMAN=AM.AN.cos0^o=AM.AN\)
\(\Rightarrow\dfrac{AH}{AM}=\dfrac{AN}{AH}\Rightarrow\Delta ANH\sim\Delta AHM\left(c-g-c\right)\)
\(\Rightarrow\widehat{ANH}=\widehat{AHM}=90^o\)
\(\Rightarrow\Delta ANH\) vuông tại \(N\)
\(\Rightarrow N\) thuộc đường tròn đường kính \(AH\)
19.
a, Ta có \(\overrightarrow{OM}.\overrightarrow{OA}=OM.OA.cos\widehat{MOA_i}=R^2.\widehat{MOA_i}\left(i\in\left\{1;2;...;n\right\}\right)\)
\(\Rightarrow cos\widehat{MOA_i}=\dfrac{1}{R^2}.\overrightarrow{OM}.\overrightarrow{OA}\)
Khi đó
\(cos\widehat{MOA_1}+cos\widehat{MOA_2}+...+cos\widehat{MOA_n}=\dfrac{1}{R^2}\overrightarrow{OM}.\left(\overrightarrow{OA_1}+\overrightarrow{OA_2}+...+\overrightarrow{OA_n}\right)=0\)
b, Theo định lí cosin:
\(cos\widehat{MOA_i}=\dfrac{OM^2+OA_i^2-MA_i^2}{2OM.OA}=\dfrac{2R^2-MA_i^2}{2R^2}=1-\dfrac{MA^2_i}{2R^2}\)
\(\Rightarrow cos\widehat{MOA_1}+cos\widehat{MOA_2}+...+cos\widehat{MOA_n}=n-\dfrac{MA_1^2+MA^2_2+...+MA_n^2}{2R^2}=0\)
\(\Rightarrow MA_1^2+MA^2_2+...+MA_n^2=2nR^2\) có giá trị không đổi
20.
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+k\overrightarrow{BC}=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
\(\Rightarrow AM^2=\left(1-k\right)^2.AB^2+k^2.AC^2+2\left(1-k\right).k.\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\left(1-k\right)^2.c^2+k^2.b^2+2\left(1-k\right).k.AB.AC.cos\widehat{BAC}\)
\(=b^2k^2+c^2k^2-2c^2k+c^2+2\left(k-k^2\right)bc.\dfrac{b^2+c^2-a^2}{2bc}\)
\(=b^2k^2+c^2k^2-2c^2k+c^2+\left(k-k^2\right)\left(b^2+c^2-a^2\right)\)
\(=\left(k^2-k\right)a^2+kb^2+\left(k-1\right)^2\left(k^2+1\right)c^2\)