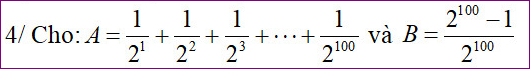\(A=\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)
\(\Rightarrow2A=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}\)
\(\Rightarrow A=2A-A=1+\dfrac{1}{2^1}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2^1}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}=1-\dfrac{1}{2^{100}}\)
\(=\dfrac{2^{100}-1}{2^{100}}=B\)
Thu gọn biểu thức đại số ta được A. -10x3y3 B. x3y3 C. 50x3y3 D. 0
Tìm x biết
1, \(\dfrac{-1}{4}-\dfrac{3}{4}:x=-\dfrac{11}{36}\)
2,\(\dfrac{3}{4}x-\dfrac{1}{2}=\dfrac{3}{7}\)
Tìm x biết
\(3\dfrac{1}{2}:0,4=x:1\dfrac{1}{7}\)
Tìm các số x, y, z biết rằng :
a. \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)và x + y - z = 38
b. 7x = 10y = 12z và x + y + z = 685
tìm x 2x-3=x+1/2
a, x : y : z = 3 : 4 : 5 và 5z^2 - 3x^2 - 2y^2 = 594
giúp mik vs mik đang gấp , bn nào trả lời chi tiết và nhanh nhất thì mik sẽ tik cho nhs
cho đa thức
A =16x4-8x3y+7x2y2-9x4 ; B= -15x4+3x3y-5x2y2-6y4 ; C = 5x3y+3x2y2+17y4+1
chứng minh một trong ba đa thức này có giá trị dương với mọi x, y
