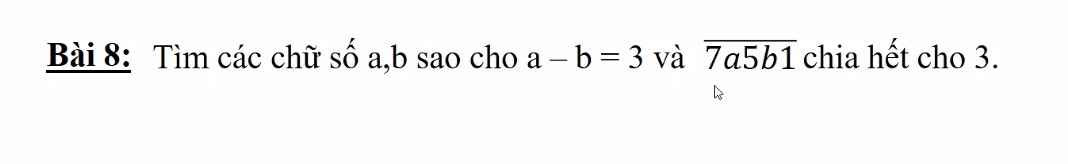Question

Answer 1

Lời giải:

Để $\overline{7a5b1}\vdots 3$ thì $7+a+5+b+1\vdots 3$ 

Hay $13+a+b\vdots 3$

$\Rightarrow a+b=\left\{2; 5; 8; 11; 14; 17; 20;....\right\}$

Mà $a+b\leq 18$ do $a\leq 9, b\leq 9$ nên:

$a+b=\left\{2;5;8;11;14;17\right\}$

Nếu $a+b=2$

$a-b=3$

$\Rightarrow b=\frac{2-3}{2}$ (vô lý)

Nếu $a+b=5$

$a-b=3$

$\Rightarrow a=4; b=1$

Nếu $a+b=8$

$a-b=3$

$a=\frac{8+3}{2}=5,5$ (loại)

Nếu $a+b=11$

$a-b=3$

$\Rightarrow a=7; b=4$

Nếu $a+b=14$

$a-b=3$

$a=\frac{14+3}{2}=8,5$ (loại)

Nếu $a+b=17$

$a-b=3$

$a=10$ (loại vì $a\leq 9$)