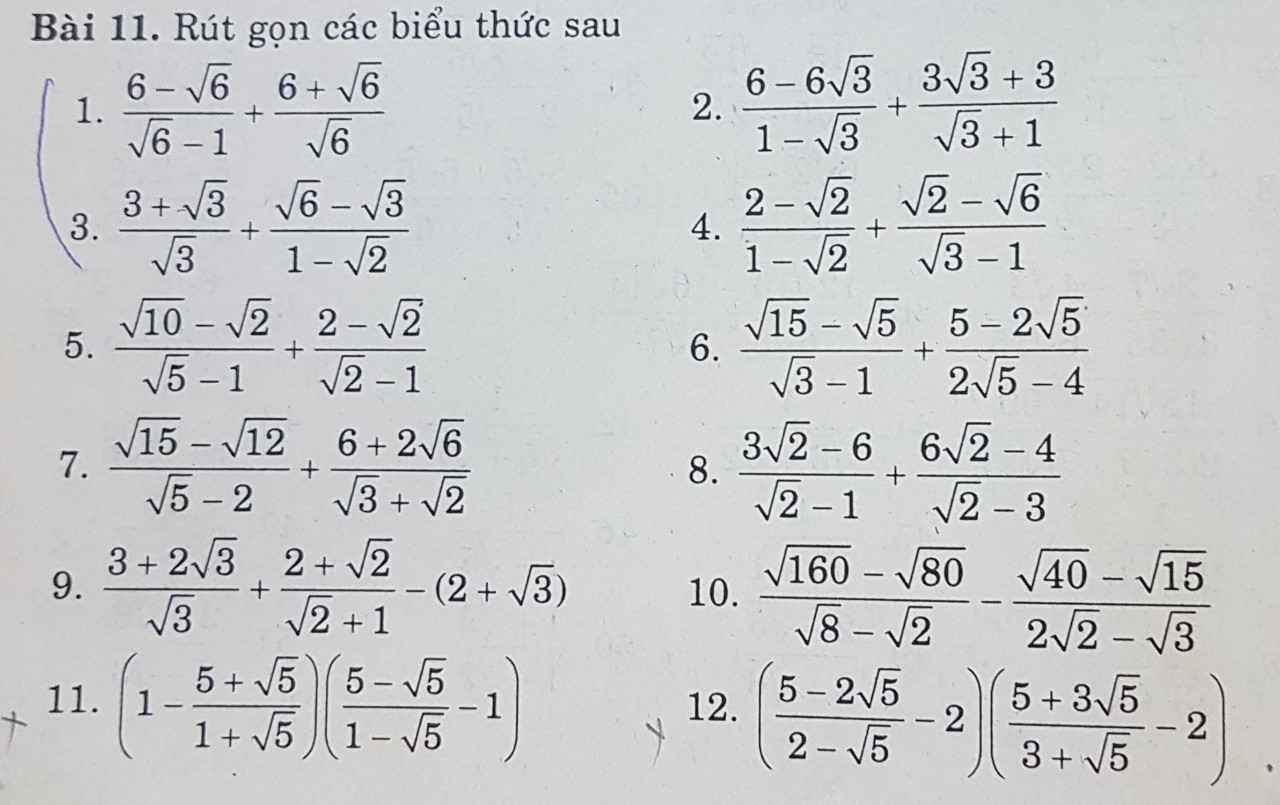1)\(\dfrac{6-\sqrt{6}}{\sqrt{6}-1}+\dfrac{6+\sqrt{6}}{\sqrt{6}}=\dfrac{\sqrt{6}\left(\sqrt{6}-1\right)}{\sqrt{6}-1}+\dfrac{\sqrt{6}\left(\sqrt{6}+1\right)}{\sqrt{6}}=\sqrt{6}+\sqrt{6}+1=1+2\sqrt{6}\)
2) \(\dfrac{6-6\sqrt{3}}{1-\sqrt{3}}+\dfrac{3\sqrt{3}+3}{\sqrt{3}+1}=\dfrac{6\left(1-\sqrt{3}\right)}{1-\sqrt{2}}+\dfrac{3\left(\sqrt{3}+1\right)}{\sqrt{3}+1}=6+3=9\)
3) \(\dfrac{3+\sqrt{3}}{\sqrt{3}}+\dfrac{\sqrt{6}-\sqrt{3}}{1-\sqrt{2}}=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+1-\sqrt{3}=1\)
4) \(\dfrac{2-\sqrt{2}}{1-\sqrt{2}}+\dfrac{\sqrt{2}-\sqrt{6}}{\sqrt{3}-1}=\dfrac{-\sqrt{2}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{-\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=-\sqrt{2}-\sqrt{2}=-2\sqrt{2}\)
Có bạn làm 1234 r nên mình làm từ bài 5 trở đi nha =))
5. \(\dfrac{\sqrt{10}-\sqrt{2}}{\sqrt{5}-1}+\dfrac{2-\sqrt{2}}{\sqrt{2}-1}=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{2}+\sqrt{2}=2\sqrt{2}\)
6. \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\dfrac{5-2\sqrt{5}}{2\sqrt{5}-4}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}=\sqrt{5}+\dfrac{\sqrt{5}}{2}=\dfrac{3\sqrt{5}}{2}\)
7. \(\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}+\dfrac{6+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}=\dfrac{\sqrt{3}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}+\dfrac{2\sqrt{3}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}=\sqrt{3}+2\sqrt{3}=3\sqrt{3}\)
8. \(\dfrac{3\sqrt{2}-6}{\sqrt{2}-1}+\dfrac{6\sqrt{2}-4}{\sqrt{2}-3}=\dfrac{3\sqrt{2}\left(1-\sqrt{2}\right)}{\sqrt{2}-1}+\dfrac{2\sqrt{2}\left(3-\sqrt{2}\right)}{\sqrt{2}-3}=-3\sqrt{2}-2\sqrt{2}=-5\sqrt{2}\)
9. \(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{\sqrt{2}+1}-\left(2+\sqrt{3}\right)=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\left(2+\sqrt{3}\right)=\sqrt{3}+2+\sqrt{2}-\left(2+\sqrt{3}\right)=\sqrt{2}\)
10. \(\dfrac{\sqrt{160}-\sqrt{80}}{\sqrt{8}-\sqrt{2}}-\dfrac{\sqrt{40}-\sqrt{15}}{2\sqrt{2}-\sqrt{3}}=\dfrac{\sqrt{2}\left(4\sqrt{5}-2\sqrt{10}\right)}{\sqrt{2}}-\dfrac{\sqrt{5}\left(2\sqrt{2}-\sqrt{3}\right)}{2\sqrt{2}-\sqrt{3}}=4\sqrt{5}-2\sqrt{10}-\sqrt{5}=3\sqrt{5}-2\sqrt{10}\)
11. \(\left(1-\dfrac{5+\sqrt{5}}{1+\sqrt{5}}\right)\left(\dfrac{5-\sqrt{5}}{1-\sqrt{5}}-1\right)=-\left(1-\sqrt{5}\right)\left(\sqrt{5}+1\right)=-1+5=4\)
12. \(\left(\dfrac{5-2\sqrt{5}}{2-\sqrt{5}}-2\right)\left(\dfrac{5+3\sqrt{5}}{3+\sqrt{5}}-2\right)=-\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)=-5+4=-1\)
Câu 3:
Ta có: \(\dfrac{3+\sqrt{3}}{\sqrt{3}}-\dfrac{\sqrt{6}-\sqrt{3}}{\sqrt{2}-1}\)
\(=\sqrt{3}+1-\sqrt{3}\)
=1
Câu 1
Ta có: \(\dfrac{6-\sqrt{6}}{\sqrt{6}-1}+\dfrac{6+\sqrt{6}}{\sqrt{6}}\)
\(=\sqrt{6}+\sqrt{6}+1\)
\(=2\sqrt{6}+1\)